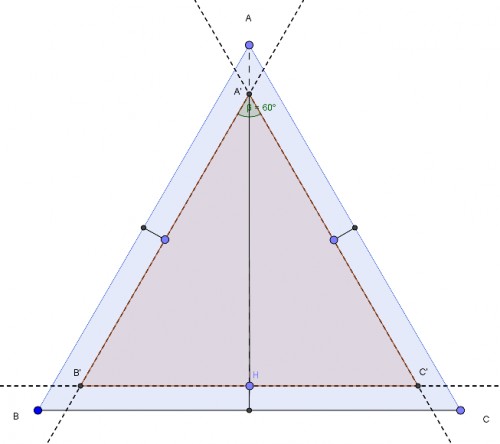
همانطور که در شکل مشاهده می کنید محل اصابت در منطقه ای قرار میگیرد که مثلث $A'B'C'$ نامیده شده است که مثلثی متساوی الاضلاع است که اضلاع آن در موازات یک واحدی اضلاع مثلث $ABC$ با ارتفاع 15 و به کمک فیثاغورس به طول ضلع $10 \sqrt{3} $ قرار گرفته است .مثلث $A'B'C'$ دارای ارتفاع 12 و طول ضلع $8 \sqrt{3} $ میشود که به این ترتیب احتمال این اصابت برابر است با:
$ P= \frac{ S_{ \triangle A'B'C'} }{S_{ \triangle ABC}}= \frac{\frac{64 \times 3 \sqrt{3} }{4}}{ \frac{100 \times 3 \sqrt{3} }{4} }= \frac{64}{100}=0/64 $