رابطهٔ تعداد درختها در یکای مکانتان (در پرسش شما جریب) و تعداد سیبهایشان با توجه به دادههای پرسش یک تابع دوضابطهای به شکل زیر میشود؛
$$\left\{\begin{array}{ll}600x & ;\,x\leq 20\\
(600-15(x-20))x & ;\,x>20\end{array}\right.$$
متوجه شدن بخش یکم تابع سخت نیست. بخش دوم نیز سخت نیست ولی تنها برای آن دسته که ممکن است ایده را نگرفته باشند؛ در پرسش تعداد سیبهای هر درخت با تعداد سیبهای درخت دیگر برابر در نظر گرفته شده است (و یا منطقیتر میانگین آنها به عنوان این پارامتر در نظر گرفته شده است). زمانی که بیشتر از ۲۰ درخت داشته باشید به ازای هر درخت افزودهتر یعنی به تعداد $x-20$ تا پانزدهتا از این تعداد متوسط سیب هر درخت کاسته میشود پس این پارامتر برابر میشود با $600-(x-20)15$ و در پایان نیز تعداد سیبهای کل درختان واقع در یکای مکان مدنظر است پس باید متوسط سیبهای یک درخت را در تعداد درحتهای موجود در یکای مکانمان ضرب کنیم که ضابطهٔ دوم تابعمان بدست میآید.
اکنون نقاط نامزد برای اتخاذ بیشینهها و کمینهها را مییابیم. ابتدا و انتهای بازهها و نقاطی که تابعمان مشتق ندارد یا مشتقش صفر است را در یک مجموعه گرد میآوریم. ضابطهٔ یکم مشتقپذیر و با مشتق همهجا ناصفر است، صفر و بیست نیز ابتدا و انتهای بازه هستند (چه در ۲۰ مشتقپذیر باشد تابعمان چه نباشد چون انتها و ابتدای بازه است باید بیاید لذا بررسی کردن مشتقپذیری تابعمان در این نقطه کاری اضافه است). ضابطهٔ دوم برابر است با $900x-15x^2$. مشتق آن برابر با $900-30x$ میشود و در $x=30$ صفر میشود. اکنون جدول تغییرات تابعمان را مینویسیم.
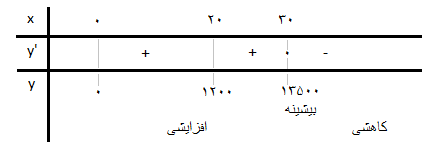
پاسخ ۳۰ درخت در جریب است.