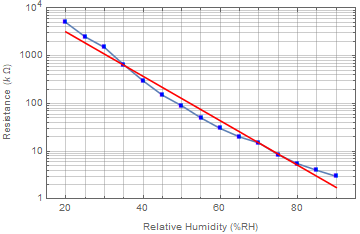
چون دادههایتان را دقیق ندارم، از روی نمودارتان تقریبشان را برمیدارم. ابتدا برای آن دسته از کاربرانی که شاید ندانند درجهبندی روی نمودارهای محورلگاریتمی چگونه تعبیر میشوند باید بگویم که به محور $y$های شکل آمده در پرسش نگاه کنید. از پائین شروع میکنیم. ۱، عددی که لگاریتمش صفر است، شروع محور است. توجه کنید که اعداد منفی و صفر لگاریتم حقیقی ندارند! پس زمانی از محور لگاریتمی استفاده میکنیم که دادههای این محور مثبت هستند. در نتیجه ۱ مبدأ این محور است، اعداد بزرگتر از ۱ بالای آن و اعداد بین صفر و یک زیر آن، دقیقا متناظر با مثبت، صفر و منفی بودن لگاریتمشان. اولین تیکی که میبینید عدد ۲ است، سپس ۳، تا ۹ که نزدیک به تیک مربوط به عدد ۱۰ است. در درجهبندی معمولی دو تفاوت داشتیم، یکی اینکه فاصلهٔ درجههای یکی بود، دیگری اینکه بین هر دو واحد اصلی ۹ تیک بود، یعنی بین ۰ و ۱۰ تعداد تیکها ۹ تا بود، همینطور بین ۱۰ تا ۲۰ و الی آخر. اما در درجهبندی لگاریتمی فاصلهٔ تیکها هر چه به واحد بعدی نزدیکتر میشویم کمتر میشود و تعداد تیکها نیز ۸ تا است، بین ۱ و ۱۰ فقط ۸ تیک است که عددهای ۲ تا ۹ را نشان میدهند. سپس بین ۱۰ و ۱۰۰ نیز ۸ تیک است که عددهای ۲۰ تا ۹۰ را نشان میدهند. امیدوارم این توضیح برای خواندن محور $y$های شکل پرسش به اندازهٔ کافی روشن باشد. پس برای نمونه نخستین نقطهٔ سمت چپ چون روی چهارمین تیک بعد از ۱۰۰۰ است عدد ۵۰۰۰ را نشان میدهد. برخی نقطهها دقیقا (یا تقریبا) روی تیکِ خاصی نیستند، نقطهٔ دوم بین تیکهای یکم و دوم بعد از ۱۰۰۰ هستند. من میانگین ۲۰۰۰ و ۳۰۰۰ را برایش برداشتم ولی این کار اشتباهی است، من صرفا برای سریعتر انجام کار این کار را کردم، ولی خوانندهای که میخواهد روش درست را پیش بگیرد باید دقیقا همان درجهبندیای که ابتدا فاصلهٔ بیشتر دارد و سپس فاصلهٔ تیکها کمتر میشود را با ۸ قسمت بین دو تیک در نظر بگیرید و زیرتیکها را مشخص کند، بنابراین من احتمال میدهم عدد ۲۶۰۰ دقیقتر باشد. به هر حال. عددهایی که من برای این ۱۵ نقطه انتخاب کردم را از چپ به راست در زیر آوردهام.
$$\lbrace 5000,2500,1500,650,300,150,90,50,30,20,15,8.5,5.5,4,3\rbrace$$
بازکِشیِ نمودار شما با دادههای گزینش شدهٔ من با کمک نرمافزار Mathematica که دستور انجام آن را هم در زیر آوردهام به شکل زیر میشود.
X = ConstantArray[0, 15];
For[i = 1, i <= 15, i++,
X[[i]] = 20 + (i - 1)*5;
];
Y = {5000, 2500, 1500, 650, 300, 150, 90, 50, 30, 20, 15, 8.5, 5.5, 4, 3}
data = {};
For[i = 1, i <= 15, i++,
AppendTo[data, {X[[i]], Y[[i]]}];
];
plot1 = ListLogPlot[data, PlotRange -> {{15, 95}, {1, 10000}}, Joined -> True,
PlotMarkers -> Style["\[FilledSquare]", Small, Blue], GridLines -> Full]
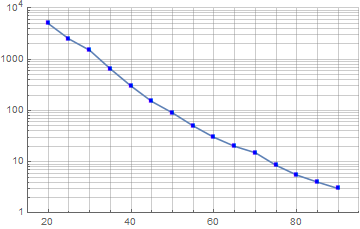
همانطور که میبینید یک مقدار خیلی کمی در برخی نقطهها تفاوت دارد که به دلیل حدس زدن دادهٔ $y$-ِ نقطههایتان است. اما برویم سراغ هدف اصلی. توجه کنید که در این نمودار، چشمِ شما در حال مشاهدهٔ نقطههای $(x,\log y)$ هستید نه نقطههای $(x,y)$! پس اگر فکر میکنید نمودار این دادهها شبیه به نمودار خاصی است، باید $\log$ را در آن تأثیر دهید. برای نمونه من فکر میکنم این نمودار به یک خط نزدیک است. پس میخواهم یک ضابطهٔ خطی به آن نسبت بدهم به شکل $ax+b$. چیزی که باید توجه کنم این است که $y$ نیست که به این شکل دیده میشود، بلکه $\log y$ است. پس داریم:
$$\log y=ax+b\Longrightarrow y=10^{ax+b}$$
میتوانم از ابتدا از این شکل استفاده کنم و پارامترهای $a$ و $b$ را برازش کنم، ولی چون کار با چیزهای خطی معمولا سادهتر است یک متغیر کمکی تعریف و آن را به کار میگیرم. تعریف میکنم $z=\log y$. در اینصورت دارم $z=ax+b$. پیش از ادامهٔ خواندن این متن اگر با رگرسیون و برازش پارامترها آشنایی ندارید، ابتدا این پاسخ (روی این پیوند کلیک کنید) را که پیشتر برای پرسش دیگری گذاشتهبودم را بخوانید. تابع برازشگرمان را به شکل زیر که همان جمع مجذور خطاها است تعریف میکنیم (که البته زیراندیس $i$ برای $x$ و $z$ ها را با فرض اینکه خودتان متوجه هستید نگذاشتهام و جمعها نیز از $i=1$ شروع و به $n$ که در اینجا ۱۵ است پایان مییابند).
$$\begin{align}
f(a,b) &= \sum(z-ax-b)^2\\
&= \sum(z^2+a^2x^2+b^2-2axz-2bz+2abx)\\
&= (\sum x^2)a^2+nb+2(\sum x)ab-2(\sum xz)a-2(\sum z)b+(\sum z^2)
\end{align}$$
چون تابع برازشگرمان نامنفی است پس دارای کمینه (نه الزاما مطلق، برای اطمینان از وجود کمینهٔ مطلق باید شرطهای بیشتری داشتهباشیم) است. در اینجا یک چندجملهای درجهٔ دو بر حسب $a$ و $b$ شدهاست که در نتیجه کمینهٔ مطلق خودش را هم اتخاد میکند. چون پیوسته است پس اکسترممهای آن نقاطی هستند که مشتق جزئیای صفر شود (اگر ناپیوسته باشد باید نقطههای ابتدا و انتهای بازه یا در چند بعدی مزرهای دامنه را هم بررسی کرد). پس مشتقهای جزئی را تشکیل دهیم.
$$\left\lbrace\begin{array}{l}
\frac{\partial f}{\partial a}=2(\sum x^2)a+2(\sum x)b-2(\sum xz)\\
\frac{\partial f}{\partial b}=2nb+2(\sum x)a-2(\sum z)
\end{array}\right.$$
اگر خوب به این دو عبارت نگاه کنید با مساوی صفر قرار دادن آنها یک دستگاه خطی دومعادله دومجهول دارید و حل کردن آن سادهاست. به هر حال محاسبهٔ جمعها و حل این دستگاه را با نرمافزار Mathematica انجام دادم و دستور نوشتهشده را در زیر میتوانید ببینید. و توجه کنید که باید $z_i$ها یعنی $\log y_i$ها را استفاده کنید!
Solve[2*Sum[X[[i]]^2, {i, 1, 15}]*a + 2*Sum[X[[i]], {i, 1, 15}]*b -
2*Sum[X[[i]]*Log10[Y[[i]]], {i, 1, 15}] == 0 &&
2*15*b + 2*Sum[X[[i]], {i, 1, 15}]*a -
2*Sum[Log10[Y[[i]]], {i, 1, 15}] == 0, {a, b}, Reals]
حاصل نمایش دادهشده در نرمافزار Mathematica تا چندین رقم اعشار به شکل زیر است.
$$a=-0.046550839779568136`,b=4.433332523006432`$$
که علامت $`$ در انتهای عددها در نرمافزار Mathematica اعلامکنندهٔ تقریب بودن این عددها است. پس یک پیشنهاد برای ضابطه برای تابعی که نمودارش تقریبی از نمودار شما باشد، تابع زیر است.
$$y=10^{(-0.046)x+(4.433)}$$
یا شاید بهتر باشد به این شکل ساده کنیم.
$$y=(27122.7)(0.898357)^x+e$$
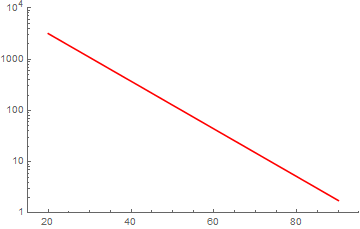
که $e$ نشاندهندهٔ جملهٔ خطا است. نمودار این تابع را در صفحه با محور $y$-ِ لگاریتمی میتوان با دستور زیر در Mathematica رسم کرد.
plot2 = LogPlot[
10^(-0.046550839779568136`*x + 4.433332523006432`), {x, 20, 90},
PlotRange -> {{15, 95}, {1, 10000}}, PlotStyle -> Red]
و برای نمایش هر دو نمودار رویهم میتوانید از دستور زیر استفاده کنید.
how[plot1, plot2, Frame -> True,
FrameLabel -> {"Relative Humidity (%RH)",
"Resistance " ToExpression["(k \\Omega )", TeXForm, HoldForm]}]