Question

به ازای چه مقادیری از $m$ نمودار تابع با ضابطهٔ $y=2x^2+x+3m-1$ از هر چهار یک‌چهارمِ صفحهٔ مختصات می‌گذرد؟

Answer 1

یک برابریِ درجهٔ دو دارید. اگر این برابری هیچ ریشه‌ای نداشته‌باشد، آنگاه همواره مثبت یا همواره منفی است پس هر نقطهٔ $(x,y)$ای که بر روی این نمودار بردارید، $y$-ِ آن همیشه مثبت یا همیشه منفی است. یعنی کل نمودار یا بالای محور $x$ها است یا کل آن زیر این نمودار است. در هر دو حالت شما دو تا از یک‌چهارم‌های صفحهٔ مختصات را از دست خواهید داد. پس باید حتما یک ریشه داشته‌باشد. اگر دقیقا یک ریشهٔ حقیقی داشته‌باشد، آنگاه (بحث تعیین علامت از یکُم دبیرستان را به یاد آورید)، همواره نامنفی (یعنی مثبت و صفر فقط) یا همواره نامثبت (یعنی منفی و صفر فقط) خواهد بود، از نظر شکلی، یعنی بر محور $x$ها در یک نقطه مماس است و کل نمودار به جز آن یک نقطه بالا یا کل آن پائین محور است. پس در این حالت نیز دو یک‌چهارم را از دست‌خواهید داد. پس تا اینجا ثابت شد که حالت‌های بدون ریشه یا با یک ریشه نامناسب هستند.

اکنون دوباره بنا به همان بحث تعیین علامت، علامتِ $y$ زمانی که $x$ بیرون دو ریشه هم‌علامت ضریب پیشرو و درون آن دو، خلاف علامت ضریب پیشرو خواهدبود. اگر هر دو ریشه در سمتِ راستِ محور $y$ها باشند (یعنی این دو ریشه مثبت باشند) آنگاه در سمتِ چپِ محورِ $y$ها تمامِ $(x,y)$هایی که روی نمودار هستند، $y$هایشان یک علامت یکسان دارند، پس همه‌شان یا در یک‌چهارمِ بالایی یا در یک‌چهارمِ پائینیِ سمت چپ هستند، یعنی یکی از یک‌چهارم‌ها خالی می‌ماند. در نتیجه هر دو ریشه نیاید در سمت راست باشند. به روش یکسان می‌بینید که هر دو هم نمی‌توانند سمت چپ باشند. پس تا اینجا ثابت شد که نه تنها باید دو ریشه داشته‌باشیم، بلکه یکی باید سمت راست و دیگری سمت چپ محور $y$ها باشد. این یعنی دو ریشهٔ برابریِ درجهٔ دویمان باید یکی مثبت و دیگری منفی باشند. ناهمعلامت بودن دو عدد ناصفر هم‌ارز است با منفی بودن ضرب‌شان. پس دو شرطی که پیدا کردیم برای تابعِ $y=ax^2+bx+c$ برابر می‌شوند با

1. $\Delta=b^2-4ac > 0$
2. $\frac{c}{a} < 0$ (به یاد آورید که حاصلضرب دو ریشهٔ یک برابریِ درجهٔ ۲ برابر با $\frac{c}{a}$ می‌شد).

اینک این دو شرط را برای برابری‌تان بررسی می‌کنیم.

$$\begin{array}{l} \Delta>0 \Rightarrow 1-8(3m-1)>0\\ \frac{c}{a}<0 \Rightarrow \frac{3m-1}{2}<0 \end{array}$$

نابرابریِ نخست به ما $m<\frac{24}{9}$ و دومی به ما $m<\frac{1}{3}$ را می‌دهد. پس باید $m<\min(\frac{24}{9},\frac{1}{3})$ باشد که می‌شود $m<\frac{1}{3}$. برای نمونه صفر در این بازه است و تابع‌تان را $y=2x^2+x-1$ می‌کند که نمودارش در زیر آمده‌است.

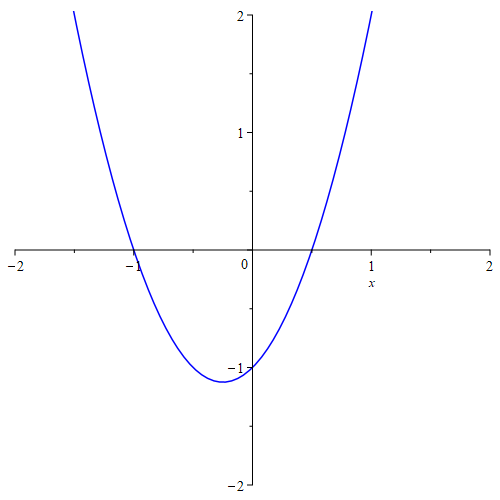
همان‌گونه که می‌بینید با هر چهار یک‌چهارم اشتراکِ ناتهی دارد.

Answer 2

وقتی تابع از هر چهار ناحیه میگذره که x های مثبتی باشند که با جایگذاری y های مثبت و منفی بدست بیاید . و x های منفی باشد با جایگذاری y های مثبت و منفی بدست بیاید . در پاسخ بالا وقتی x خارج از محدوده 2 ریشه باشد y مثبت خواهد بود . و اگر عددی میان 2 ریشه تابع باشد y منفی خواهد بود پس باید یکی از ریشه های ما مثبت و دیگری منفی باشد در غیر اینصورت ما ورودی منفی یا مثبتی نخواهیم داشت که خروجی منفی تحویل بدهد .

حال طبق قضیه ویت اگر $a$ و $b$ ریشه های تابع بالا باشند $ab= \frac{3m-1}{2} $ پس $3m-1$ باید منفی باشد. در نتیجه $ \frac{1}{3} > m$