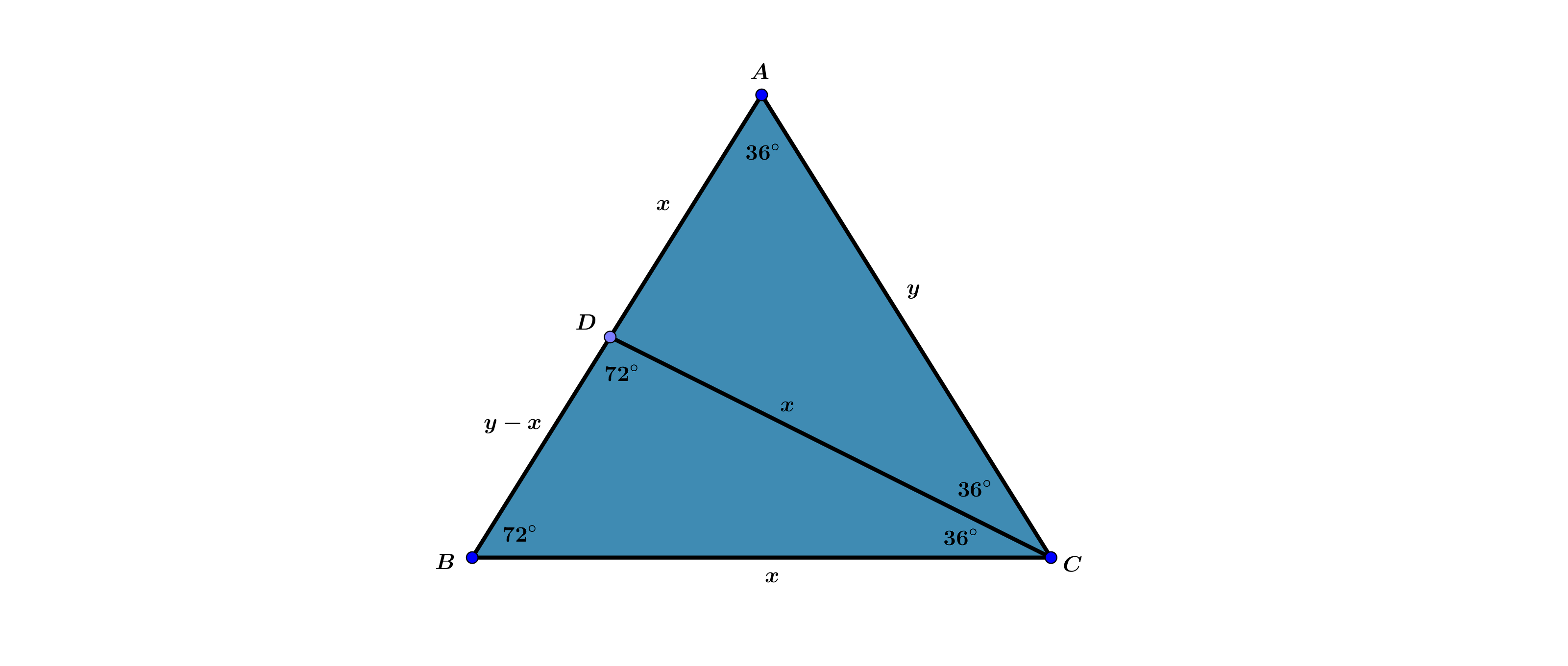
همانطور که از شکل پیداست مثلث $ \triangle ABC $ با مثلث $ \triangle BDC$ متشابه است
چرا ؟ (برابری سه زاویه ) در نتیجه خواهیم داشت :
$$\dfrac{x}{y}=\dfrac{y-x}{x}$$
$$y^2-xy-x^2=0$$
معادله درجه دو برحسب $y$ داریم که با حل آن :
$$y=\dfrac{x\pm \sqrt{x^2-4(-x^2)}}{2}=\dfrac{x\pm x\sqrt5}{2}=\dfrac{x(1\pm\sqrt5)}{2}$$
اما چون طول همواره مثبت است فقط یک حالت داریم :
$$y=\dfrac{(\sqrt5+1)x}{2}$$
از خاصیت مثلث متساوی الساقین که ارتفاع و نیمساز و عمود منصف نظیر قاعده باهم برابر هستند استفاده میکنیم . خواهیم داشت :
:
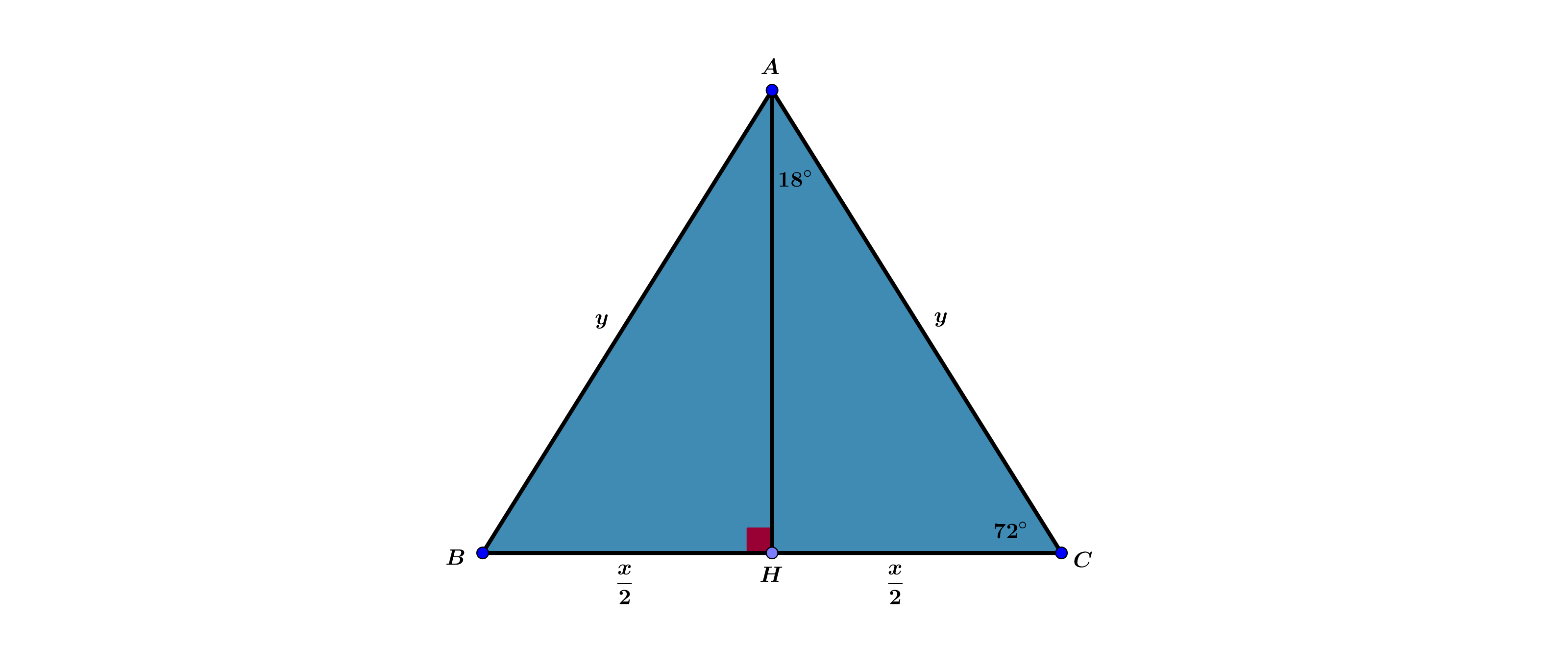با توجه به شکل خواسته سوال را بدست میاوریم
$$\sin 18^ \circ =\dfrac{\dfrac{x}{2}}{y}=\dfrac{\sqrt{5}-1}{4}$$
