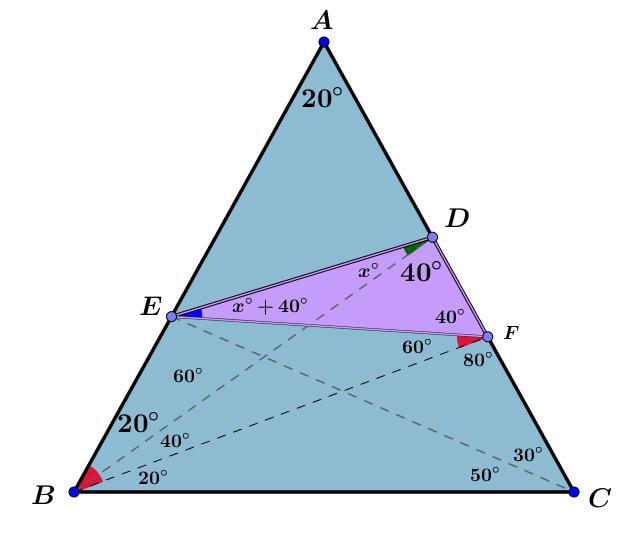
در هفت مرحله جواب را بدست می آوریم :
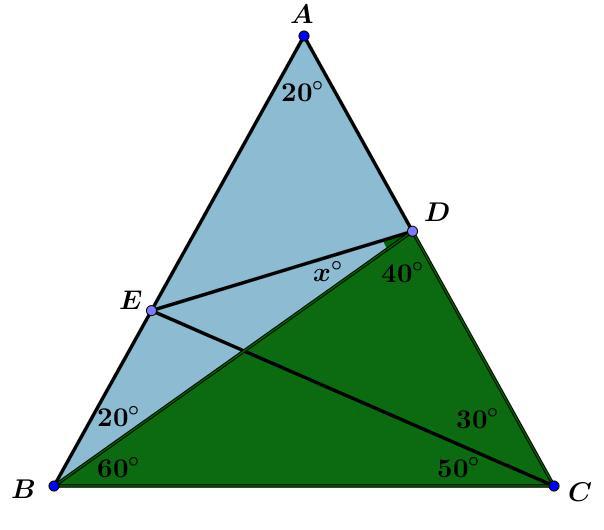
مرحله صفر : شکل را رسم میکنیم .
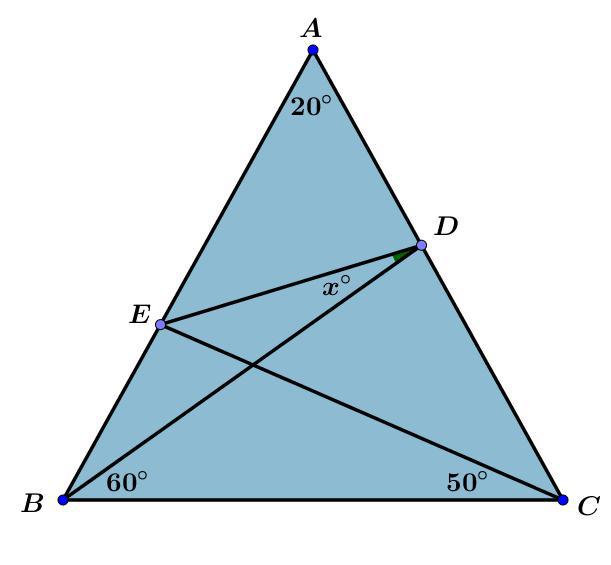
مرحله یک : چون مثلث متساوی الساقین است در نتیجه
$$ \angle ABC= \angle ACB=80^ \circ $$ .
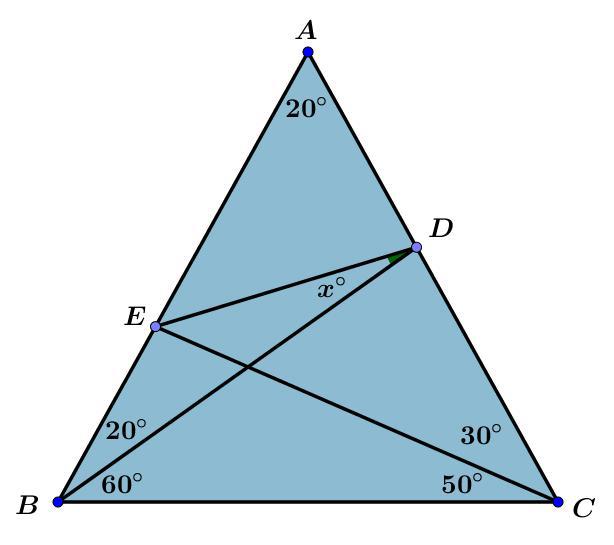
مرحله دو : مثلث $ \triangle EBC$ را در نظر بگیرید . میدانیم که مجموع زوایه های داخلی مثلث برابر $180^ \circ $ در نتیجه
$$ \angle BEC= 50^ \circ \Rightarrow |BE|=|BC|$$ .
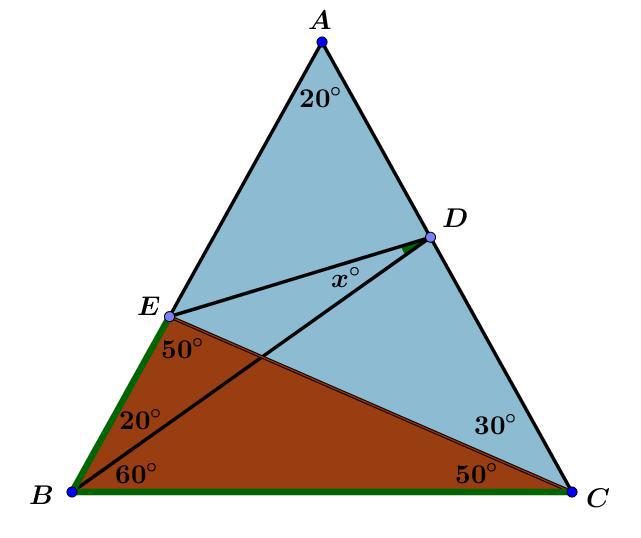
**مرحله سه ** :مثلث $ \triangle BDC$ را در نظر بگیرید . میدانیم که مجموع زوایه های داخلی مثلث برابر $180^ \circ $ در نتیجه
$$ \angle BDC= 40^ \circ $$ .
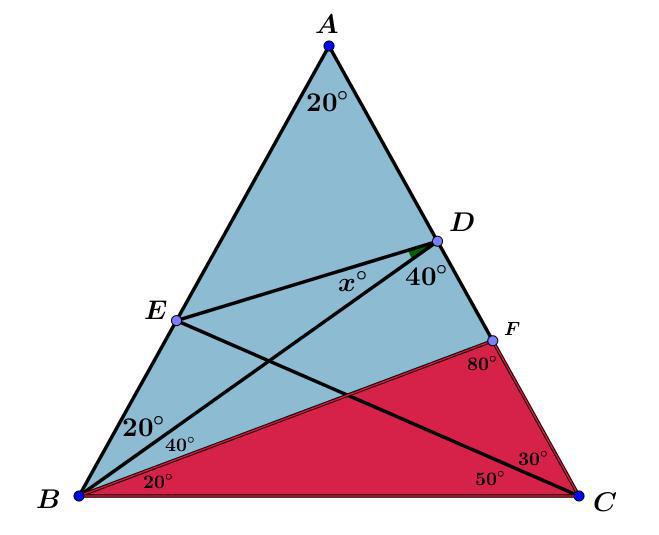
**مرحله چهار ** : زاویه $ \angle DBC= 60^ \circ $ در نظر بگیرید به دو زاویه
$20^ \circ ,40^ \circ $
تقسیم میکنیم به طوری که :
$$ \angle FBC= 20^ \circ , \angle DBF= 40^ \circ $$ .
در نتیجه خواهیم داشت :
$$ \angle BFC= 80^ \circ \Rightarrow |BF|=|DF|$$ .
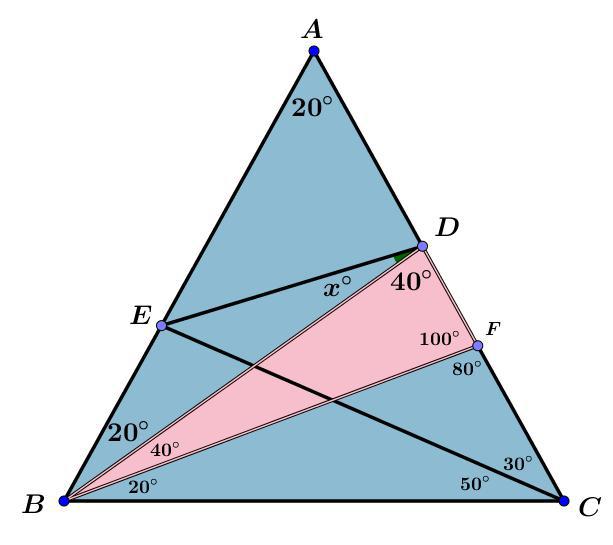
مرحله پنج : مثلث $ \triangle DBF $ در نظر بگیرید دو زاویه برابر دارد
$ \angle DBF=40^ \circ ,\angle BDF=40^ \circ $ در نتیجه مثلث متساوی الساقین است و داریم
$$ \angle DFB= 100^ \circ , |BF|=|DF|$$ .
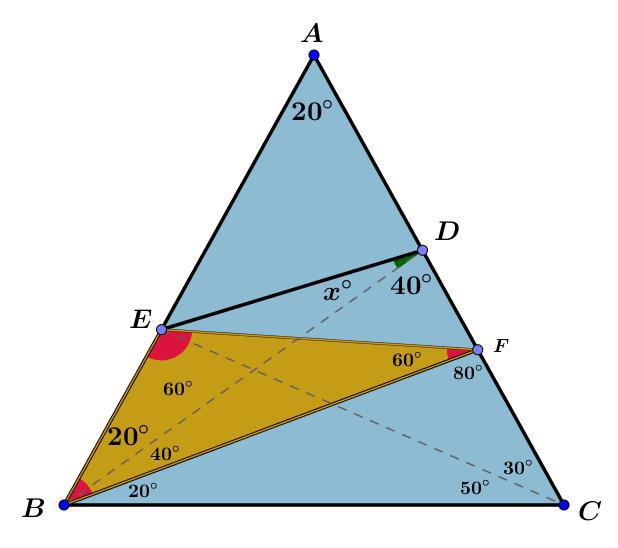
مرحله شش : نقطه $F$ را به نقطه $E$ متصل میکنیم مثلث $ \triangle EBF $ ایجاد میشود .
در مرحله دو فهمیدیم که $|BE|=|BC|$
و در مرحله چهار فهمیدیم که $|BF|=|BC|$
در نتیجه
$$ |BE|=|BF|, \angle BEF= 60^ \circ =\angle EFB= 60^ \circ \Rightarrow $$
بنابر این
$$|BE|=|BF|=|EF|$$
**مرحله هفت ** :
در مرحله پنج فهمیدیم که $|BF|=|DF|$
و در مرحله شش فهمیدیم که $|BE|=|BF|=|EF|$
در نتیجه
$$ |EF|=|DF|$$
پس مثلث $ \triangle EDF $ متساوی الساقین است .
و از مرحله شش میدانیم که :
$\angle DFE= 40^ \circ $
و اطلاع داریم مجموع زاویه های داخلی مثلث برابر $180^ \circ $
بنابر این
$$2(x^ \circ +40^ \circ )+40^ \circ =180^ \circ \\ x^ \circ =30^ \circ $$