ظاهرا در مورد تعیین دامنه خودتان پاسخ را میدانید (از متن پرسشتان مشخص است). پس یکراست به سراغ نرمافزار Mathematica میرویم. حدس من این است که از دستورِ Plot استفاده میکنید. در این صورت باید بدانید که برای نمایش فرجهٔ $n$اُم در نرمافزار Mathematica سه راه دارید. اگر ریشهٔ دوم است از Sqrt و اگر ریشهٔ سوم است از CubeRoot استفاده کنید. این روش یکُم بود. روش دوم استفاده از دستورِ Surd است که دو ورودی دارد، یکُمی برای چیزی که از آن میخواهید ریشهٔ $n$اُم بگیرید و دومی عددِ $n$. روش سوم استفاده از توان کسری است. چون فرض خاصی روی تابع $f(x)$ نمیخواهید لحاظ کنید برای نمونهٔ این پست تابع بدیهی همانی یعنی $f(x)=x$ را برمیدارم. پس سه بار نمودار ضابطهٔ $y=\sqrt[3]{x}$ را از Mathematica درخواست میکنم. هر سه دستور را به همراه شکل رسمشده برایشان را در زیر میگذارم (هر شکل پس از دستورش گذاشتهشدهاست).
Plot[CubeRoot[x], {x, -5, 5}]
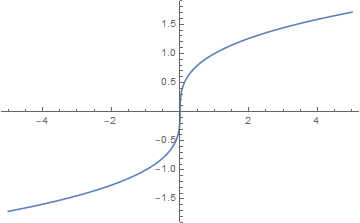
Plot[Surd[x, 3], {x, -5, 5}]
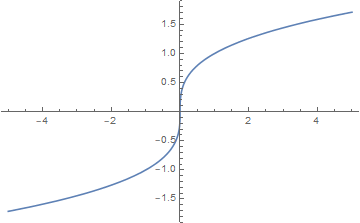
Plot[x^(1/3), {x, -3, 3}]
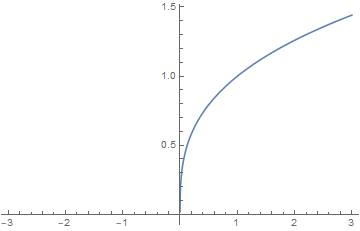
پس نرمافزار Mathematica میتواند شکل را رسم کند ولی برای این کار باید از دو روش نخست برای نمایش فرجه استفاده کنید نه توان کسری (علت عدم رسم در قسمت منفی باید در الگوریتم توان کسری در Mathematica باشد که در پست آمده در پانویس اینجا میتوانید بخوانید ).
روش دیگر برای رسم نمودار مورد نظر استفاده از ترسیم نگاشتهای ضمنی یعنی استفاده از دستورِ ContourPlot به جای استفاده از Plot است. این دستور، مجموعهترازِ یک ضابطهٔ دومتغیره را رسم میکند، که تراز مورد نظر را با کمک تساوی (دوعلامت مساوی) به آن باید بدهید. دستور مربوطه و شکل مورد نظر در زیر آمدهاند. توجه کنید که
$$\lbrace (x,y)\mid y=\sqrt[3]{x}\rbrace=\lbrace (x,y)\mid y^3=x\rbrace$$
ContourPlot[y^3 - x == 0, {x, -5, 5}, {y, -5, 5}]
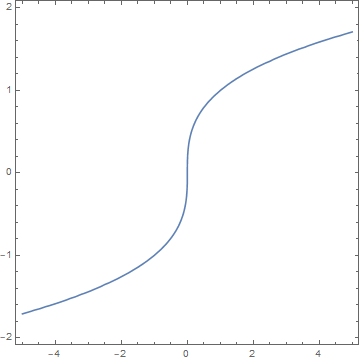
همینگونه که میبینید، در این حالت نیز مشکلی با قسمت منفی زیر رادیکال نیست.