برای رسم نمودار سهبعدی در GeoGabra نخست باید به ماشینحساب سهبعدیاش بروید. توجه کنید که مارپیچ ارشمیدس یک منحنی در فضای سهبعدی دارای تاب است پس در صفحهٔ دوبعدی آن را نباید رسم کنید مگر اینکه تصویرش بر روی یک صفحه را مدنظر داشتهباشید. پس من به جای رفتن به آدرس
https://www.geogebra.org/graphing?lang=en
به آدرس سهبعدیاش یعنی
https://www.geogebra.org/3d?lang=en
میروم. سپس در سمت چپ دستور زیر را تایپ میکنم:
(cos(t),sin(t),t), (-18<=t<=18)
در ابتدای دستور مختصات یک نقطهٔ دلخواه از مارپیچ ارشمیدس را که بر حسب یک پارامتر یعنی $t$ پارامتریشدهاست را وارد کردهام، سپس یک فاصله گذاشتهام و در داخل پرانتز بازهای که میخواهم پارامترم در آن تغییر کند را میگذارم. توجه کنید که زمانی که کوچکتری و سپس مساوی تایپ میکنید خودکار برایتان آن دو را ترکیب و به $\leq$ تغییر میدهد. خروجیتان به شکل زیر سمت چپ میشود. البته من با موشواره شکل را در سمت راست صفحه دوران و zoom-out کردهام. میتوانید دستور زیر را نیز تایپ کنید که رسمیترِ همان ورودی بالا است.
Curve((cos(t),sin(t),t),t,-18,18)
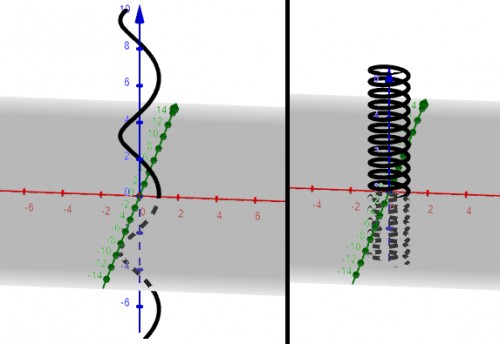
ضابطهٔ پارامتری بالا (که شما ضابطهٔ دکارتی میگوئید) در واقع این است که طول و عرض نقطهها در مسیر محیط دایرهٔ واحد در حال حرکت هستند که زاویهٔ خط متصلکنندهٔ این نقطه یعنی $(x,y)$ به مرکز این دایرهٔ دوبعدی واحد با ارتفاع نقطه یعنی $z$-ِ آن مشخص میشود. شکل شبیه به یک فنر است که خیلی کشیدهشدهاست. با تغییر نحوهٔ ارتباط زاویهٔ حرکت با ارتفاع میتوانید این فنر (یا مارپیچ) را فشردهتر یا بازتر کنید. برای نمونه اگر در داخل $\cos$ و $\sin$ به جای $t$ از $10t$ استفاده کنید به شکل سمت راست زیر میرسید.
Curve((cos(10*t),sin(10*t),t),t,-18,18)