فرمولهای زیادی برای رابطهٔ بین یک عدد مختلط چه در مختصات دکارتی چه در مختصات قطبی و ریشههایش میتوانید بنویسید. برای چند نمونه میتوانید به پیوند زیر نگاه بیندازید.
پیوند به چند نمونه فرمول برای جذر اعداد مختلط
کاری که شما باید انجام بدهید (با هر نرمافزار یا زبان برنامهنویسی) این است که نمایش اعداد مختلط دامنه و همدامنه را انتخاب و سپس فرمول نگاشتتان (ضابطهتان در اینجا به هر نقطه، دو نقطه تصویر میکند پس تابع نیست) که از نمایش نقاط دامنه به نمایش تصویر تابع در آن نقاط در همدامنه میرود را بنویسید و سپس به نرمافزار بدهید یا برنامهنویسی کنید که نقاط رسم شوند.
من اینطور عمل کردم؛
برای دامنه از نمادهای $z=x+iy=re^{i\theta}$ و برای همدامنه از نمادهای $f(z)=u+iv=se^{i\theta}$ استفاده کردم. یک نقطه از دیسک واحد به شکلِ $re^{i\theta}$ نوشته میشود که $0\leq r\leq 1$ (توجه کنید که دیسک واحد باز یا بسته همهاش تنها در مرز دایره فرق میکند، شما میتوانید مساوی سمت یک را حذف کنید) و $0\leq \theta\leq 2\pi$. اگر با نمایشهای اعداد مختلط آشنا باشید با یک سادهسازی ساده دارید؛
$$se^{i\phi}=f(re^{i\theta})= \sqrt{(1+r\cos\theta)+i(r\sin\theta)}$$
دوباره با توجه به اینکه جذر گرفتن از یک عدد مختلط در مختصات قطبی برابر با نصف کردن زاویه و جذر گرفتن از اندازه و قرار دادن یک مثبتمنفی است با کمک رابطهٔ نمایش اعداد مختلط و کمی سادهسازی میفهمید که؛
$$s=\pm\sqrt{\sqrt{r^2+1+2r\cos\theta}},\quad \phi=\frac{1}{2}\arctan(\frac{r\sin\theta}{1+r\cos\theta})$$
و
$$u=s\cos\phi,\quad v=s\sin\phi$$
از طرفی برای خود دامنه هم داریم؛
$$x=r\cos\theta,\quad y=r\sin\theta$$
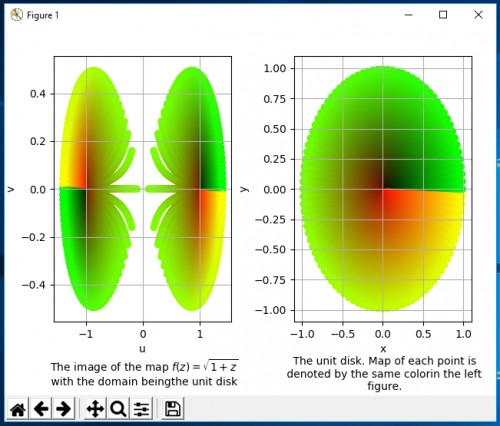
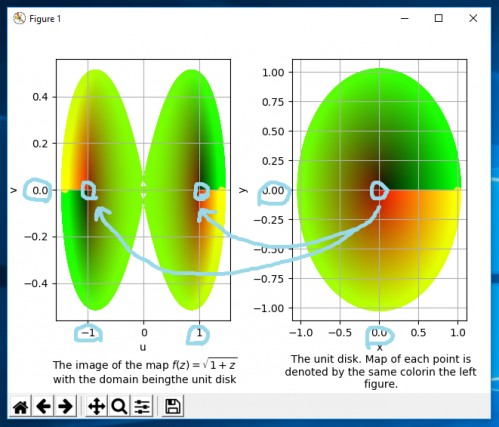
پس برای رسم نمودار در Python به صورت کاملا از پایه (تنها از توابع sqrt و arctan2 و sin و cos که در library پیشفرضِ math در Python موجود هستند استفاده کردم) و با نقطهنقطه نگاری برای تعداد $10^4$ نقطه (یعنی بازهٔ $[0,1)$-ِ $r$ را ۱۰۰ قسمت و بازهٔ $[0,2\pi)$ -ِ $\theta$ را نیز ۱۰۰ قسمت مساوی و سپس $(x,y)$ و $(u,v)$ را با رابطههای بالا برای هر انتخاب از $(r,\theta)$ محاسبه) بوسیلهٔ library نگارندهٔ matplotlib شکل یکُم را رسم کردم که کمتر از یک ثانیه اجرایش طول میکشد. در سمت راست دامنه را میبینید و در سمت چپ تصویر تابع از این دامنه. تصویر هر نقطه دو نقطه است که با همان رنگ نمایش داده شده است، پس میتوانید نقاط را دنبال کنید. مثلا وقتی قرار میدهید $z=0$ دارید $f(z)=\pm 1$ که در شکل سوم با فلشهای نیلیرنگ مشخص کردم.
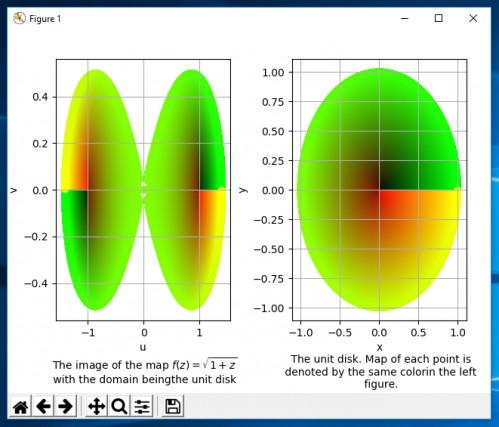
برای اینکه پیوستگی شکل بیشتر بشود و به کل شکل نزدیکتر شویم باید مقدار تقسیمبندیها را افزایش دهیم. شکل دوم برای $10^6$ یعنی هر یک از بازههای $r$ و $\theta$ ۱۰۰۰ بخش، میباشد. البته مدت زمان محاسبات ۱۰۰ برابر میشود پس تقریبا یک دقیقه وقت نیاز است ولی مشکل اصلی بحث گرافیکی میشود که کمی برای پایتون سنگین میشود (امکان گرفتن پیام خطای not responding وابسته به مشخصات رایانهتان هست).
یک نکتهٔ مهم دیگر این است که زمانیکه دیسک باز را در نظر میگیرید نقطهٔ $(0,0)$ را در تصویر نخواهید داشت (چون تصویر نقطهٔ $(-1,0)$ است که بر روی مرز دیسک قرار دارد و این تنها نقطهٔ وصل کنندهٔ دو شاخهٔ راست و چپ تصویر است. بسادگی میتوانید ثابت کنید که تصویر دیسک باز توسط این نگاشت ناهمبند میشود.
اگر چیزی به نظرتان در شکل درست نیست، لطفا خبر دهید تا کد را بازبینی کنم.