ЩҲШ§Ш¶Шӯ Ш§ШіШӘ Ъ©ЩҮ ЩҮЩ…ЩҮ ЫҢ Щ…Ш«Щ„Ш« ЩҮШ§ ШҜШ§ШұШ§ЫҢ ШҜШ§ЫҢШұЩҮ Щ…ШӯЫҢШ·ЫҢ ЩҮШіШӘЩҶШҜ. ШІЫҢШұШ§ Щ…ЫҢ ШҜШ§ЩҶЫҢЩ… Ъ©ЩҮ Ш№Щ…ЩҲШҜЩ…ЩҶШөЩҒ ЩҮШ§ЫҢ ЩҮШұ ШіЩҮ Ш¶Щ„Ш№ Щ…Ш«Щ„Ш« ЩҮЩ…ШұШі Ш§ЩҶШҜ ЩҲ ЩҒШ§ШөЩ„ЩҮ ЩҶЩӮШ·ЩҮ ШӘЩӮШ§Ш·Ш№ Ш№Щ…ЩҲШҜЩ…ЩҶШөЩҒ ЩҮШ§ Ш§ШІ ШіЩҮ ШұШ§Ші Щ…Ш«Щ„Ш« ШЁШұШ§ШЁШұЩҶШҜ ЩҫШі Щ…ЫҢ ШӘЩҲШ§ЩҶЫҢЩ… ШҜШ§ЫҢШұЩҮ Щ…ШӯЫҢШ·ЫҢ ШұШіЩ… Ъ©ЩҶЫҢЩ….
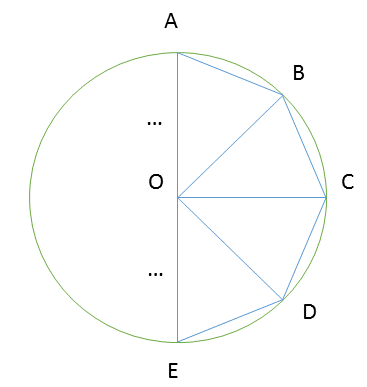
ЩҮЩ…ЪҶЩҶЫҢЩҶ Щ…ЫҢ ШӘЩҲШ§ЩҶ Ш«Ш§ШЁШӘ Ъ©ШұШҜ ЩҮШұ ЪҶЩҶШҜ Ш¶Щ„Ш№ЫҢ Щ…ЩҶШӘШёЩ… ШҜШ§ШұШ§ЫҢ ШҜШ§ЫҢШұЩҮ Щ…ШӯЫҢШ·ЫҢ Ш§ШіШӘ. ШЁШұШ§ЫҢ Ш§Ш«ШЁШ§ШӘ ШЁЩҶШ§ШЁШұ ЩҶЪ©ШӘЩҮ ЫҢ ШЁШ§Щ„Ш§ Щ…ЫҢ ШӘЩҲШ§ЩҶЫҢЩ… ЫҢЪ© ШҜШ§ЫҢШұЩҮ Ш§ШІ ШіЩҮ ЩҶЩӮШ·ЩҮ $A,B,C$ ЪҜШ°ШұШ§ЩҶШҜ. ЩҫШі ШЁЩҶШ§ШЁШұШӘШ№ШұЫҢЩҒ ШҙШ№Ш§Ш№ ШҜШ§ЫҢШұЩҮ $OB=OC$ ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ $\angle OBC=\angle OCB$ Ш§Щ…Ш§ ЪҶЩҲЩҶ ЪҶЩҶШҜШ¶Щ„Ш№ЫҢ Щ…ЩҶШӘШёЩ… ШҜШ§ШұЫҢЩ… ЩҫШі ШӘЩ…Ш§Щ…ЫҢ ШІЩҲШ§ЫҢШ§ ШЁШ§ ЩҮЩ… ШЁШұШ§ШЁШұЩҶШҜ ЩҫШі Ш§ШІ $\angle B=\angle C$ ШҜШ§ШұЫҢЩ… $\angle OBA=\angle OCD$ Щ„Ш°Ш§ ШЁЩҶШ§ШЁШұ ШӯШ§Щ„ШӘ ШҜЩҲ Ш¶Щ„Ш№ ЩҲ ШІШ§ЩҲЫҢЩҮ ШЁЫҢЩҶ Щ…Ш«Щ„Ш« ЩҮШ§ЫҢ $\triangle OAB$ ЩҲ $\triangle OCD$ ЩҮЩ… ЩҶЩҮШҙШӘ ЩҮШіШӘЩҶШҜ. ЩҲ Ш§ЫҢЩҶ Ш«Ш§ШЁШӘ Щ…ЫҢ Ъ©ЩҶШҜ $OA=OB=OC=OD$ ЩҲ ШЁЩҮ ЩҮЩ…ЫҢЩҶ ШӘШұШӘЫҢШЁ Щ…ЫҢ ШӘЩҲШ§ЩҶЫҢЩ… ЩҶШҙШ§ЩҶ ШҜЩҮЫҢЩ… ЩҮЩ…ЩҮ ШұШ§Ші ЩҮШ§ЫҢ ЪҶЩҶШҜШ¶Щ„Ш№ЫҢ Щ…ЩҶШӘШёЩ… ШұЩҲЫҢ ШҜШ§ЫҢШұЩҮ ЩӮШұШ§Шұ ШҜШ§ШұЩҶШҜ. ЩҫШі Ш§ЫҢЩҶ ШҜШ§ЫҢШұЩҮ ШЁШұ ЪҶЩҶШҜШ¶Щ„Ш№ЫҢ Щ…ШӯШ§Ш· Ш§ШіШӘ.