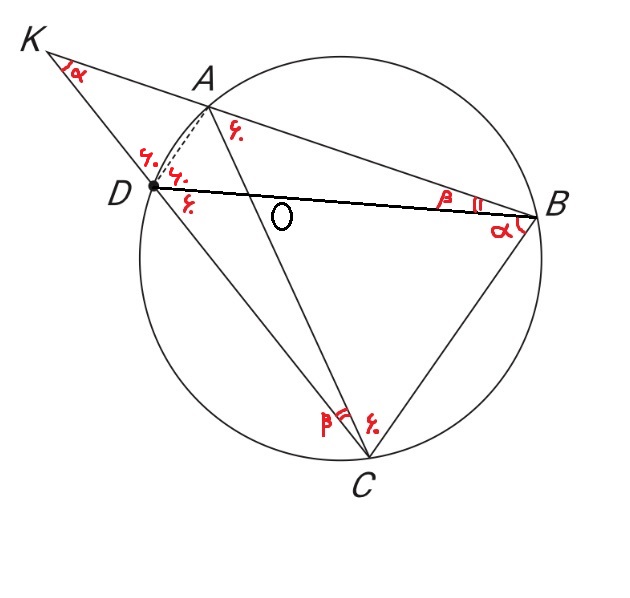
طول ضلع مثلث متساوی الاضلاع محاط در دایره برابر جذر 3 ضربدر شعاع است.
$AB=AC=BC=r \sqrt{3} $
DO+OB=5 , KD=3
بنابر قانون کسینوس ها
$KB^{2} = 5^{2} + 3^{2} −2×5×3×cos120$
KB=7
مثلث های KDB , KAC مشابهند در نتیجه
$ \frac{KA}{3} = \frac{r \sqrt{3} }{5} $
از طرفی $KA+r \sqrt{3} =7$
$ \frac{7-r \sqrt{3} }{3} = \frac{r \sqrt{3} }{5} $
پس:
$KA= \frac{21}{8} , r = \frac{35}{8 \sqrt{3}} , AB= \frac{35}{8} $
دوباره قانون کسینوسها در مثلث ADB :
$ \frac{35}{8} ^{2} = AD^{2} + 5 ^{2} −2×AD× 5 ×cos60 $
پس:
َAD=1.875
ضمنا یک جواب $ \frac{25}{8} $ هم بدست می آید که صحیح نیست. زیرا با این عدد قانون کسینوس ها در مثلث KDA درست بدست نمی آید.