ابتدا با سه نکته شروع میکنیم :
1-)اگر روی یک پاره خط دلخواه $AC$ نقطه ایی مانند $B$ قرار دهیم .با رابطه زیر میتوان مختصات نقطه $B$ را بدست بیاوریم .
2-) مرکز ثقل مثلث مثلث را به نسبت $ 2:1 $ قطع میکند .
3-) میانه، به پارهخطی میگویند که از یک راس مثلث به وسط ضلع روبرو کشیده میشود.
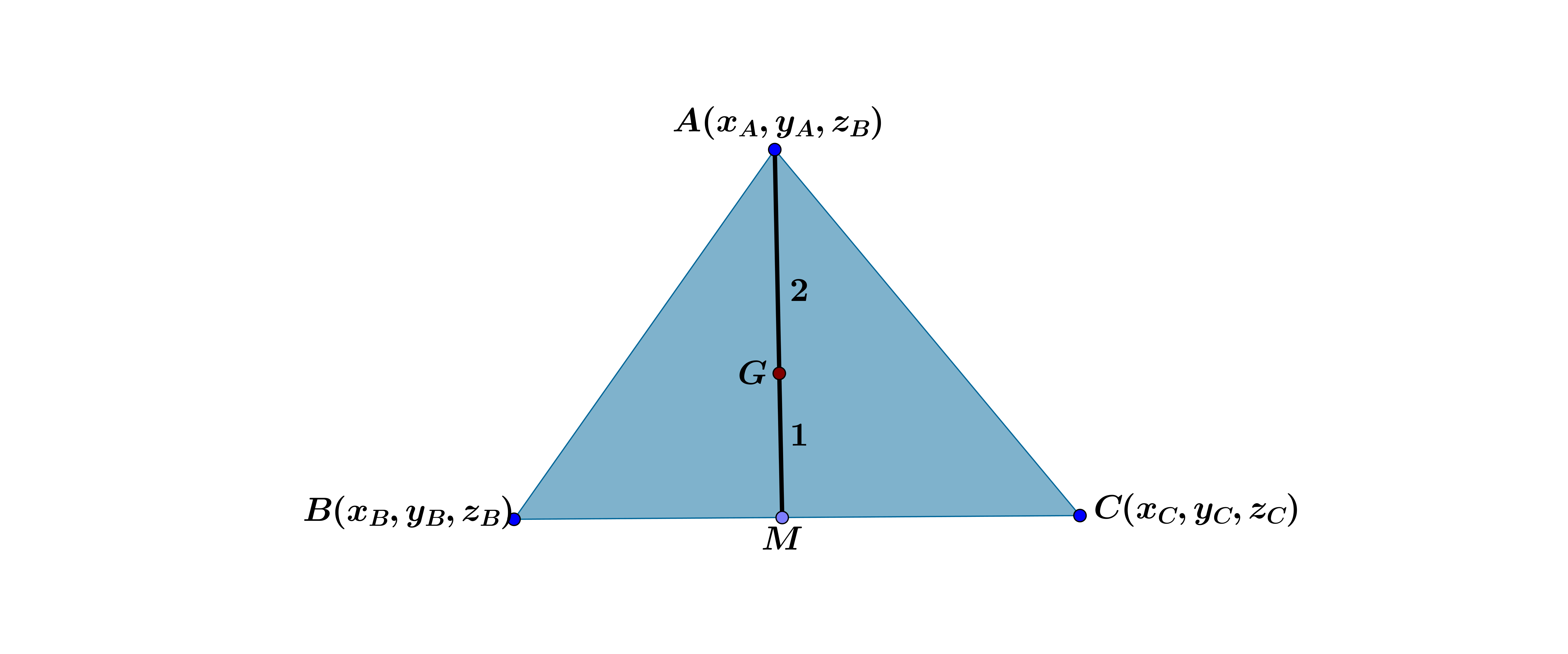حالا با توجه به شکل میریم سراغ حل سوال :
$$x_{M}= \frac{x_{B}+x_{C}}{2} $$
$$x_{G}= \frac{2x_{M}+x_{A}}{3} $$
جایگذاری :
$$x_{G}= \frac{x_{B}+x_{C}+x_{A}}{3} $$
$y_{G},z_{G}$ به همین صورت بدست می آوریم :
$$y_{G}= \frac{y_{B}+y_{C}+y_{A}}{3} $$
$$z_{G}= \frac{z_{B}+z_{C}+z_{A}}{3} $$
اثبات تمام . شاد باشید .
