فرض کنید مختصات سه نقطه معلوم عبارتند از: $(x_1, y_1)$، $(x_2, y_2)$ و $(x_3, y_3)$
میخواهیم مختصات مرکز $(x_c, y_c)$ و شعاع $r$ دایره گذرا از این سه نقطه را بیابیم. چون این سه نقطه روی یک دایره قرار گرفته اند با توجه به معادله دایره داریم:
$$(x_1 - x_c)^2 + (y_1 - y_c)^2 = r^2 (1)$$
$$(x_2 - x_c)^2 + (y_2 - y_c)^2 = r^2 (2)$$
$$(x_3 - x_c)^2 + (y_3 - y_c)^2 = r^2 (3)$$
از $(1)$ و $(2)$ نتیجه می گیریم:
$$(x_1 - x_c)^2 + (y_1 - y_c)^2 = (x_2 - x_c)^2 + (y_2- y_c)^2 (4)$$
و از $(2)$ و $(3)$ نتیجه می گیریم:
$$(x_2 - x_c)^2 + (y_2 - y_c)^2 = (x_3 - x_c)^2 + (y_3- y_c)^2 (5)$$
و از $(1)$ و $(3)$ نتیجه می گیریم:
$$(x_1 - x_c)^2 + (y_1 - y_c)^2 = (x_3 - x_c)^2 + (y_3- y_c)^2 (6)$$
با بسط و ساده سازی معادلات $(4)$، $(5)$ و $(6)$ داریم:
\begin{cases}
2(x_2-x_1)x_c+2(y_2-y_1)y_c= x_2^2-x_1^2+y_2^2-y_1^2\\
2(x_3-x_2)x_c+2(y_3-y_2)y_c= x_3^2-x_2^2+y_3^2-y_2^2&&(7)\\
2(x_3-x_1)x_c+2(y_3-y_1)y_c= x_3^2-x_1^2+y_3^2-y_1^2\end{cases}
حال متغیرهای زیر را تعریف میکنیم:
$$a_1=2(x_2-x_1), b_1=2(y_2-y_1), c_1=x_2^2-x_1^2+y_2^2-y_1^2$$
$$a_2=2(x_3-x_2), b_2=2(y_3-y_2), c_2=x_3^2-x_2^2+y_3^2-y_2^2$$
$$a_3=2(x_3-x_1), b_3=2(y_3-y_1), c_3=x_3^2-x_1^2+y_3^2-y_1^2$$
با قرار دادن مقادیر فوق در $(7)$ داریم:
\begin{cases}a_1 x_c+b_1 y_c=c_1\\
&&(8)\\
a_2 x_c+b_2 y_c=c_2\end{cases}
\begin{cases}a_2 x_c+b_2 y_c=c_2\\
&&(9)\\
a_3 x_c+b_3 y_c=c_3\end{cases}
\begin{cases}a_1 x_c+b_1 y_c=c_1\\
&&(10)\\
a_3 x_c+b_3 y_c=c_3\end{cases}
$(8)$، $(9)$ و $(10)$ دستگاه های 2 معادله 2 مجهولی ساده هسند. با حل هر یک از این دستگاه ها مختصات مرکر دایره $(x_c,y_c)$ بدست می آید. مثلاً حل $(8)$ منجر می شود به:
$$x_c= \frac{c_1 b_2 - c_2 b_1}{a_1 b_2 - a_2 b_1} (11)$$
$$y_c= \frac{c_2 a_1 - c_1 a_2}{a_1 b_2 - a_2 b_1} (12)$$
بدیهی است که معادله های $(11)$ و $(12)$ وقتی دارای جواب هستد که:
$$a_1 b_2 - a_2 b_1\neq 0 (13)$$
اگر شرط $(13)$ برقرار نبود بدین معناست که هیچ دایره ای از این سه نقطه عبور نمیکند یعنی این نقاط روی یک خط راست قرار دارند.
با داشتن $(x_c, y_c)$ می توان با استفاده از یکی از معادلات $(1)$ تا $(3)$ مقدار $r$ بدست آورد. مثلاً:
$$r= \sqrt{(x_1-x_c)^2+(y_1-y_c)^2} (14)$$
راه حل فوق را به یک کد تبدیل کرده ام که می توانید با استفاده از آن مختصات مرکز $(x_c, y_c)$ و شعاع دایره $r$ را بدست آورید (کد را به زبان برنامه نویسی خیام که خودم توسعه داده ام نوشته ام ولی کد بسیار واضح است و به راحتی به هر زبان برنامه نویسی دیگر قابل تبدیل است):
cls();
format("% .3Lf");
var x1, x2, x3;
var y1, y2, y3;
var fp;
var a1, b1, c1;
var a2, b2, c2;
var a3, b3, c3;
var xc, yc, r;
lprint("(x1, y1) = (");
input("X1:", x1); print(x1, ", ");
input("Y1:", y1); print(y1, ")");
lprint("(x2, y2) = (");
input("X2:", x2); print(x2, ", ");
input("Y2:", y2); print(y2, ")");
lprint("(x3, y3) = (");
input("X3:", x3); print(x3, ", ");
input("Y3:", y3); print(y3, ")");
a1 = 2*(x2 - x1);
b1 = 2*(y2 - y1);
c1 = x2^2 - x1^2 + y2^2 - y1^2;
a2 = 2*(x3 - x2);
b2 = 2*(y3 - y2);
c2 = x3^2 - x2^2 + y3^2 - y2^2;
a3 = 2*(x3 - x1);
b3 = 2*(y3 - y1);
c3 = x3^2 - x1^2 + y3^2 - y1^2;
if((a1*b2 - a2*b1) != 0)
{
xc = (c1*b2 - c2*b1)/(a1*b2 - a2*b1);
yc = (c2*a1 - c1*a2)/(a1*b2 - a2*b1);
}
else
{
lprint();
lprint("No Solution found!");
end;
}
r = sqrt((x1 - xc)^2 + (y1 - yc)^2);
lprint();
lprint("(xc, yc) = (", xc, ", ", yc, ")");
lprint(" r = ", r);
این هم همان کد به زبان فرترن:
program c3p
implicit none
real*4 x1, y1, x2, y2, x3, y3
real*4 a1, b1, c1
real*4 a2, b2, c2
real*4 a3, b3, c3
real*4 xc, yc, r
print *, "A short program for computing center and radius"
print *, "of a circle passing through 3 points"
print *, "by Ali Zokaee"
print *, "-----------------------------------------------"
print *, "enter x1:"
read *, x1
print*, "enter y1:"
read *, y1
print *, "enter x2:"
read *, x2
print *, "enter y2:"
read *, y2
print *, "enter x3:"
read *, x3
print *, "enter y3:"
read *, y3
a1 = 2.0*(x2 - x1)
b1 = 2.0*(y2 - y1)
c1 = x2**2.0 - x1**2.0 + y2**2.0 - y1**2.0
a2 = 2.0*(x3 - x2)
b2 = 2.0*(y3 - y2)
c2 = x3**2.0 - x2**2.0 + y3**2.0 - y2**2.0
a3 = 2.0*(x3 - x1)
b3 = 2.0*(y3 - y1)
c3 = x3**2.0 - x1**2.0 + y3**2.0 - y1**2.0
print *, "-----------------------------------------------"
if((a1*b2 - a2*b1) .ne. 0.0) then
xc = (c1*b2 - c2*b1)/(a1*b2 - a2*b1)
yc = (c2*a1 - c1*a2)/(a1*b2 - a2*b1)
else
print *, "No Solution could be found!"
stop
endif
r = sqrt((x1 - xc)**2.0 + (y1 - yc)**2.0)
print *, "Center Point: (xc, yc) = (", xc, ", ", yc, ")"
print *, "Radius: r = ", r
stop
end
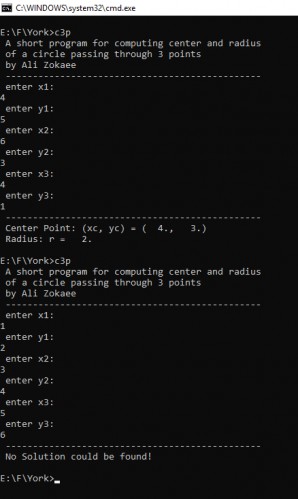
و این هم خروجی برنامه: