شکل زیر را در نظر بگیرید :
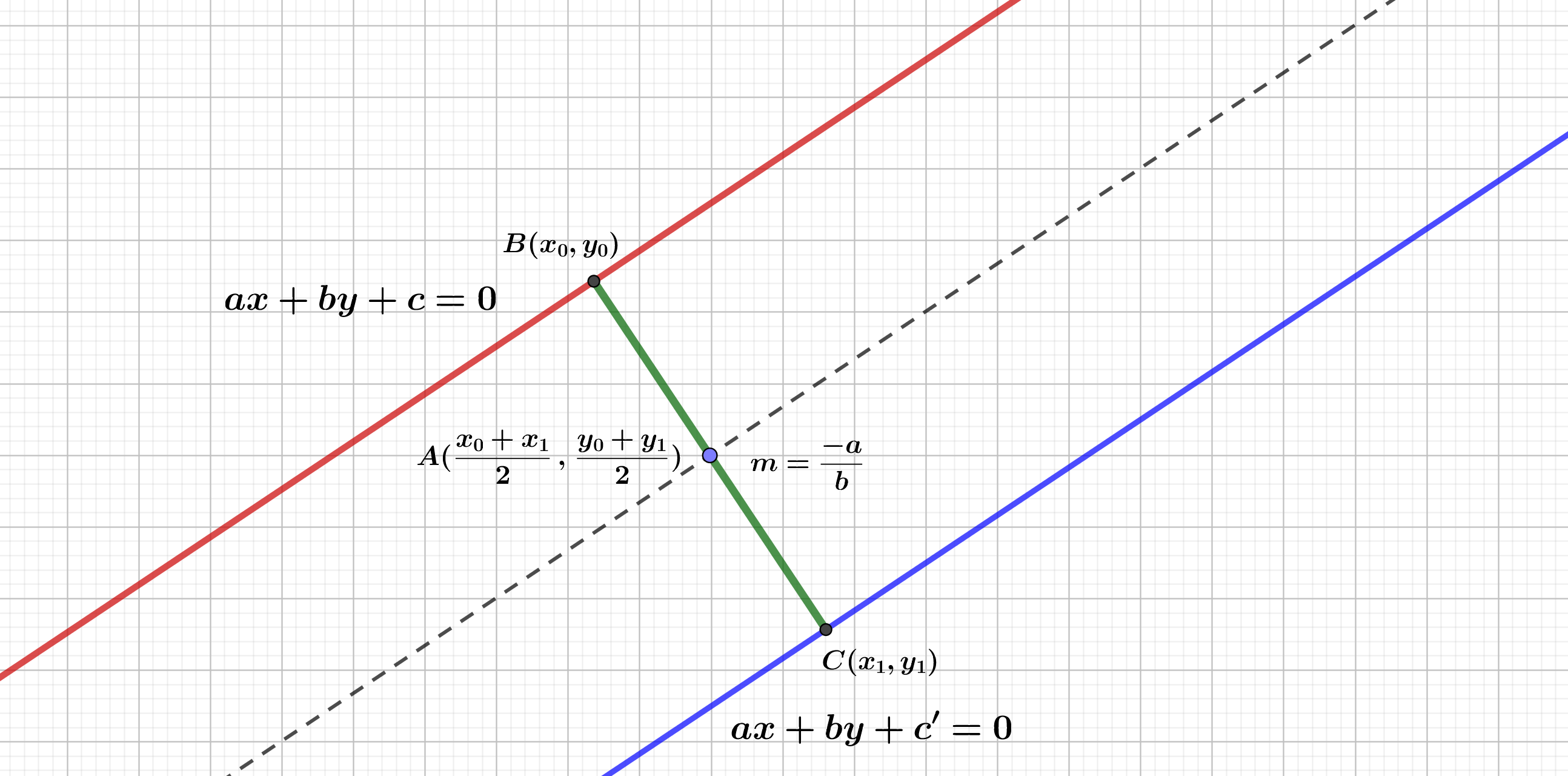
حال میدانیم که نقطه $B$ در خط $ax+by+c=0$ صدق میکند در نتیجه :
$$ax_0+by_0+c=0$$
و همچنین میدانیم که نقطه $C$ در خط $ax+by+c'=0$ صدق میکند در نتیجه :
$$ax_1+by_1+c'=0$$
حال دو معادله داریم دوتاشو با هم جمع میکنیم یعنی :
$$ax_1+by_1+c'+(ax_1+by_1+c')=0 \\ (ax_1+ax_0)+(bx_1+bx_0)+(c+c')=0 \\ a(x_1+x_0) +b(y_1+y_0)+(c+c')=0$$
حال دو طرف را تقسیم بر دو میکنیم یعنی :
$$a\frac{(x_1+x_0) }{2}+b\frac{(y_1+y_0)}{2}+\frac{(c+c')}{2}=0$$
$\frac{x_0+x_1}{2}$ طول نقاط واقع در خط وسط . وتعریف میکنیم :
$$\frac{x_0+x_1}{2}:=X$$
$\frac{y_0+y_1}{2}$ عرض نقاط واقع در خط وسط . و تعریف میکنیم :
$$\frac{y_0+y_1}{2}:=Y$$
در نتیجه :
$$aX+bY+\frac{(c+c')}{2}=0$$
و این یعنی معادله خط میانی . و اثبات کامل شد .
$\Box .$