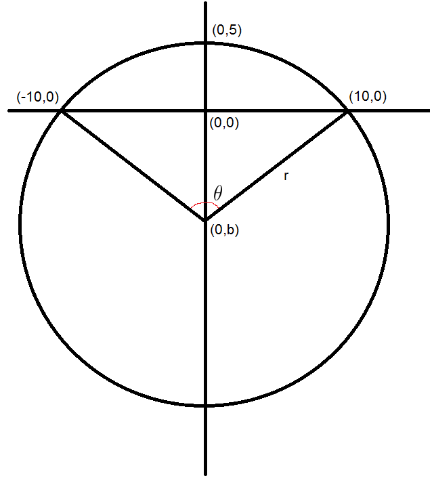
پاسخ دادن به این پرسش بسیار سادهاست و نیازی به انتگرال ندارد. بدون کاستن از کلیت حداکثر با یک انتقال در صفحه (انتقال درازای خمها را تغییر نمیدهد) میتوانید فرض کنید پارهخطتان پارهخط وصل کنندهٔ نقطههای $(10,0)$ و $(-10,0)$ است و نقطهٔ $C$ نقطهٔ $(0,5)$. نخستین چیزی که باید به ذهنتان برسد یافتن مرکز و شعاع دایره است که به ذهن یک دانشآموز یکم دبیرستانی نیز میرسد. بدون نیاز به انجام محاسبه مشخص است که درازای (طول) نقطهٔ مرکز دایره باید صفر باشد، به عبارت دیگر باید روی محور پهناها (عرضها یا همان $y$-ها) باشد. پس کارمان حتی سادهتر هم هست. سه معادله اما دو مجهول داریم! سه نقطهٔ روی دایرهمان یعنی $A$ و $B$ و $C$ را باید در $x^2+(y-b)^2=r^2$ جایگذاری کنیم. چون $a=0$ را پیش از حل میدانستیم ۳ معادله در واقع پس از نگذاشتن $a$ خودکار دو معادله شدهاند؛ $r^2-(b-5)^2=0$ و $r^2-b^2=100$ که از آنها نتیجه میشود $b=-7.5$ و $r=12.5$. میدانیم که درازای کمان روبرو به زاویهای با اندازهٔ $\theta$ رادیان، بنا به تعریف رادیان و یک نسبت و تناسب سادهٔ دبستانی-راهنمایی، برابر است با $r\theta$ باز هم نیاز به انتگرال ندارید. اما اینجا برای یافتن $\theta$ نیاز به تعریف رابطههای سهگوشی (مثلثاتی) از ریاضی دوم دبیرستان دارید. به یاد آورید که کسینوس یک زاویهٔ بین سمت مثبت محور درازاها و شعاعی در یکچهارم دوم صفحه برابر با $\pi$ منهای کسینوس زاویهٔ قرینهاش نسبت به محور پهناها میشد. پس $\theta$ برابر است با $\pi$ منهای دو برابر زاویهٔ بین سمت مثبت محور درازاها و شعاع وصل کنندهٔ مرکز دایره به نقطهٔ $(10,0)$. در نتیجه:
$$\theta=\pi-2arc\cos\frac{10}{\sqrt{10^2+7.5^2}}$$
پس درازای کمان خواستهشده برابر میشود با $(12.5)(\pi-2arc\cos\frac{10}{\sqrt{10^2+7.5^2}})$ که پاسخ دقیق است. برای تقریبش هم میتوانید از روشهای متعددی بروید برای نمونه استفاده از تقریب زدن تابع $y=arc\cos(x)$ بوسیلهٔ $y\simeq y_0+y'\mid_{x=x_0}\cdot(x-x_0)$ که این نیز در ریاضی سوم دبیرستان یا پیشدانشگاهی آموزش دادهشدهاست. به هر حال مقدار پاسخ با نرمافزار Maple تا ۸ رقم اعشار برابر است با ۲۳/۱۸۲۳۸۰۴۵.