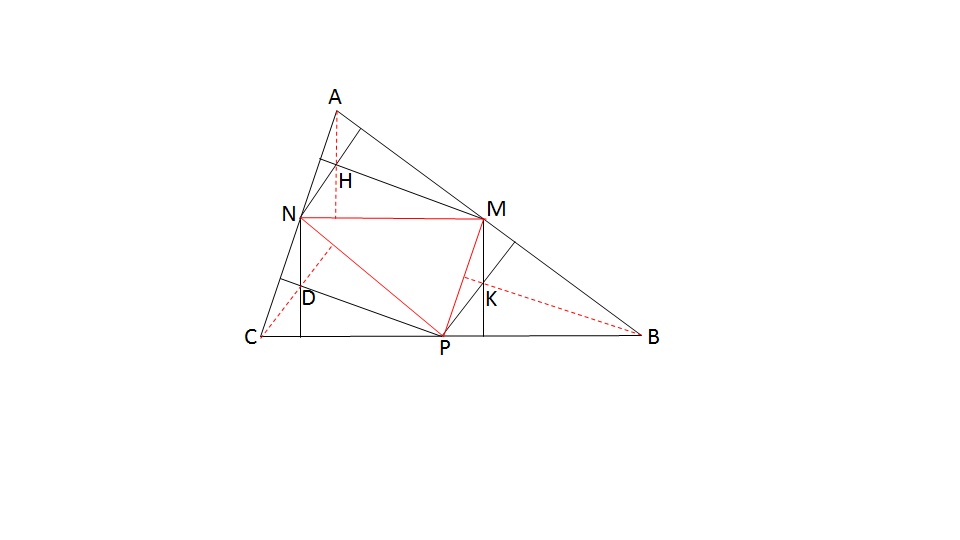
میخواهیم ثابت کنیم مساحت شش ضلعی MKPDNH نصف مساحت کل است. برای این کار وسط های اضلاع مثلث را به هم وصل میکنیم تا مثلث MPN پدید آید. مساحت مثلث MPN یک چهارم مساحت کل است پس باید ثابت کنیم مساحت بقیه ی شش ضلعی هم یک چهارم مساحت کل است.
اکنون باید توجه کنید که نقاط H , D , K به ترتیب مرکز ارتفاعی مثلث های AMN , NCP , MPB هستند. پس اگر ارتفاع سوم این مثلث ها را رسم کنیم به ترتیب بر MN , NP , PM عمود است(این ارتفاع ها به صورت نقطه چین مشخص شده اند). حال توجه کنید که سه مثلث ANM , NCP , MPB به حالت سه ضلع هم نهشتند(این مطلب به سادگی اثبات میشود). پس به ترتیب از همنهشتی مثلث های (AMN , MPB) و (NCP , MPB) میتوان نتیجه گرفت که مثلث های (HNM , KPB) و (NDP , MKB) با هم هم نهشتند. پس داریم:
1) مثلث های HNM , KPB هم نهشتند. پس مساحت آنها برابر است یعنی $S_{KPB}$=$S_{HNM}$
2) مثلث های NDP , MKB هم نهشتند. پس مساحت آنها برابر است یعنی $S_{NDP}$=$S_{MKB}$
پس میتوان نتیجه گرفت که جمع مساحت مساحت مثلث های HNM , NDP , MKP به ترتیب برابر جمع مساحت مثلث های KPB , MKB ,MKP است که این هم برابر مساحت مثلث MPB است که این هم یک چهارم مساحت کل است. و این هم همان چیزی است که می خواستیم ثابت کنیم. در حقیقت می خواستیم ثابت کنیم مساحت بقیه ی شش ضلعی یک چهارم مساحت کل است و اکنون هم ثابت شد.
خلاصه:
مساحت شش ضلعی برابر جمع مساحت مثلث های MNP , HNM , NDP , MKP است که جمع مساحت مثلث های HNM , NDP , MKP همان مساحت مثلث MPB است. یعنی مساحت شش ضلعی جمع مساحت مثلث های MNP , MPB است که مساحت هرکدام یک چهارم مساحت کل است و در نتیجه جمع مساحت آنها که همان مساحت شش ضلعی است، یک دوم مساحت کل است. پس حکم اثبات شد. تمام شد و رفت