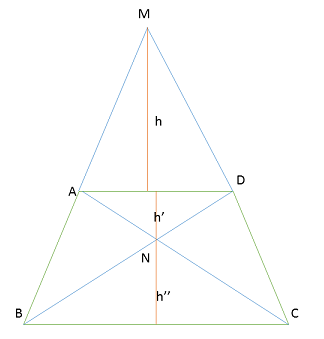
با توجه به شکل فوق داریم:
$$K=\frac{S_{AND}}{S_{AMD}}=\frac{1/2AD\times h'}{1/2ADh}=\frac {h'}h\tag{*}$$
ما به دنبال $K$ هستیم.
دو مثلث $AND$ و $BNC$ بنابر حالت سه زاویه متشابه اند و چون نسبت تشابه با نسبت ارتفاعها برابر است داریم:
$$\frac ab=\frac{h''}{h'}\tag{**}$$
اما دو مثلث $MBC$ و $MAD$ متشابه اند(سه زاویه) و چون نسبت تشابه با نسبت ارتفاعها برابر است داریم:
$$\frac{BC}{AD}=\frac{a}{b}=\frac{h+h'+h''}{h}=1+K+\frac{\frac{h''}{h'}}{\frac{h}{h'}}=1+K+\frac{\frac ab}{\frac 1k}$$
یا بطور معادل $$ \frac ab=1+k+k\frac ab $$ لذا $$k=\frac{\frac ab-1}{\frac ab+1}=\frac{a-b}{a+b}$$