نخست از E به A یک خط وصل بکنید. کمک میکند کمی وضعیت روشنتر شود.
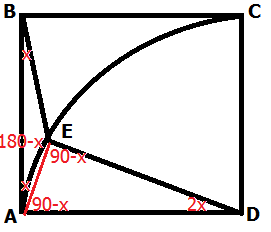
اینکه کمان AC یک ربعدایره به مرکز D و شعاع AD است این را نتیجه میدهد که پارهخط AE همدرازای پارهخط AD یعنی یال مربع است. پس یک سهگوش متساویالساقین داریم. در سهگوشهای متساویالساقین دو زاویهٔ دو گوشهٔ پای دو یال هماندازه، برابر هستند. پس اگر اندازهٔ زاویهٔ ABE را با $x$ نمایش دهیم، آنگاه زاویهٔ ADE برابر با $2x$ است (بنا به فرض پرسش). سپس هر زاویهٔ پای سهگوش ADE برابر با $\frac{180-2x}{2}$ میشود. اکنون که زاویهٔ EAD برابر با $90-x$ است پس زاویهٔ $BAE$ برابر با $90-(90-x)$ میشود. پس سهگوش AEB نیز متساویالساقین است. در نتیجه نقطهٔ E باید از دو نقطهٔ A و B یک فاصله داشته باشد.
بدون کاستن از کلیت فرض کنید A مبدأ مختصات باشد و درازای یال مربع یک باشد. مختصات نقطهٔ E را $(a,b)$ بنامید. اگر فرمول فاصلهٔ این نقطه از نقطهٔ $A=(0,0)$ و نقطهٔ $B=(0,1)$ را بنویسید و برابر قرار دهید و حل کنید به $b=\frac{1}{2}$ میرسید. اکنون از اینکه E روی دایرهٔ $(X-1)^2+Y^2=1$ قرار دارد استفاده کنید. پس $a=1-\sqrt{\frac{3}{4}}$.
اینک از E به یال AB عمودی رسم کنید. از تعریف $\tan$ داریم:
$$x=arc\tan(\dfrac{1-\sqrt{\frac{3}{4}}}{\frac{1}{2}})=arc\tan(2(1-\sqrt{\frac{3}{4}}))$$