مشخصه اویلر یعنی $ \chi $ برای چند وجهی ها برابر است با:
$$ \chi =V-E+F$$
که در آن $ V $ تعداد راس، $E $ تعداد یال و $ F $ تعداد وجه است.
برای چند وجهی های محدب این مشخصه برابر 2 است پس در توپ فوتبال این مشخصه 2 است. حال به محاسبه ی $ V$و$E $ و $F $ می پردازیم.
فرض کنید $x$ پنج ضلعی و $ y $ شش ضلعی داشته باشیم. تعداد رئوس برابر $ \frac{5x+6y}{3} $ است. تعداد یالها $ \frac{5x+6y}{2} $ و تعداد وجها برابر $ x+y $ است که با جایگذاری در معادله داریم:
$$ \frac{5x+6y}{3}-\frac{5x+6y}{2}+x+y=2 \Rightarrow \frac{x}{6}=2 $$
پس تعداد پنج ضلعی ها همواره برابر 12 است.
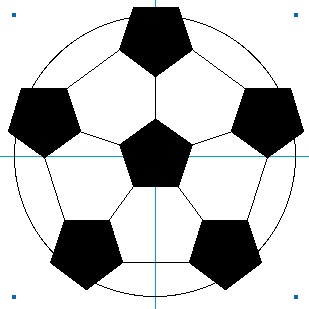
هر پنج ضلعی با 5 شش ضلعی مجاور است و هر شش ضلعی با 3 پنج ضلعی لذا تعداد شش ضلعی ها برابر است با:
$ \frac{5 \times 12}{3} =20$