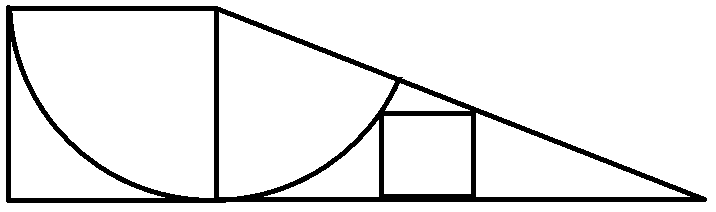
چون سهگوشِ FEC متشابه سهگوش ABC است از قضیهٔ تالس باید عددِ $k$ای وجود داشته باشد که
$$FE=k,\;EC=2k,\;FC=\sqrt{5}k$$
و چون چهارگوشِ GDEF مربع است $GD=DE=EF=FG=k$. فرض کنید مبدأ مختصات در نقطهٔ B قرار دارد. مختصات نقطهٔ G برابر است با
$$x_G=2-3k,\;y_G=k$$
از طرف دیگر این نقطه بر روی دایرهٔ به مرکز A و شعاع AB قرار دارد. مکان نقطههای روی این دایره در برابریِ $(y-1)^2+x^2=1$ صدق میکنند پس باید
$$(y_G-1)^2+x_G^2=1$$
دو یافتهٔ پیشین با هم نتیجه میدهند که $(k-1)^2+(2-3k)^2=1$ با ساده کردن یک برابریِ درجهٔ دو $10k^2-4k+4=0$ داریم. این برابری دو ریشه دارد
$$k=0.4,\;k=1$$
که $k=0.4$ مربوط به نقطهٔ G -ِ نمایش دادهشده در تصویر شماست در حالیکه $k=1$ مربوط به نقطهٔ دیگری است که هم بر روی دایره وجود دارد و هم درازا و پهنایش (طول و عرضش) با هم نسبت خواستهشده را دارند که در شکل زیر چپترین نقطهٔ بالایی است. پس پاسخ پرسش $DE=k=0.4$ است.