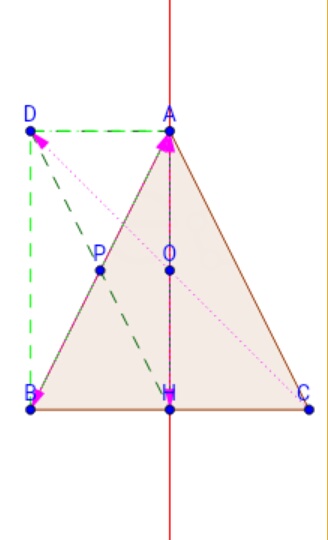
ابتدا از راس $A$ عمود بر ضلع $BC$ رسم میکنیم و نقطه عمود را $H$ می نامیم.
حال دو مثلث $AHB$ و $AHC$ بوجود می آید.
وسط دو ضلع $AH$ و $AB$ را بترتیب $O$ و $P$ می نامیم.
بازتاب مرکزی دو مثلث $AHB$ و $AHC$ را بترتیب نسبت به مرکز $P$ و $O$ بدست می آوریم.
بازتاب دو ضلع $HC$ و $HB$ از دو مثلث $AHC$ و $AHB$ برهم منطبق میشوند و چون بازتاب مرکزی ایزومتری است پس:
$$(*) HB=AD=HC$$
و از آنجا که $AH$ بر $BC$ عمود است و $(*)$ برقرار است:
پس خواص بازتاب محوری برای دو مثلث $AHB$ و $AHC$ نسبت به محور $AH$ برقرار است:
پس بازتاب محوری مثلث $AHC$ نسبت به محور $AH$ بر مثلث $AHB$ منطبق می شود و چون بازتاب زاویه $ACH$ نسبت به محور $AH$ زاویه $ABH$ می شود، پس:
$$ \widehat{ACH}= \widehat{ABH} $$