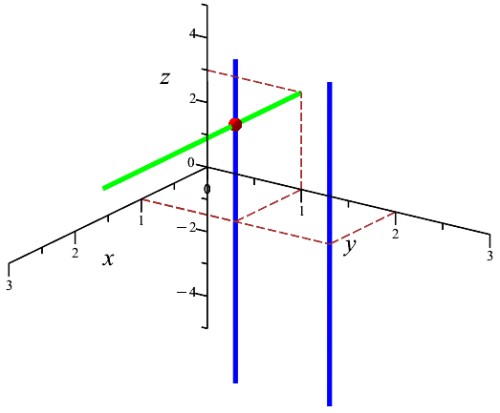
نخست اینکه تعریفِ عمود بودن دو خط را چه میگوئید؟ «دو خط را عمود بر هم گوئیم هر گاه یکدیگر را قطع کرده و زاویهٔ بین این دو خط در نقطهٔ برخورد در صفحهٔ مشترکِ این دو خط برابر با زاویهٔ راست (قائمه) یعنی $90^\circ$ باشد. اکنون آیا در هر فضای اقلیدسیِ $\mathbb{R}^n$ای اگر یک خط بر یکی از دو خطِ موازی عمود باشد، بر خط دوم نیز عمود خواهد شد؟ خیر تنها در حالتِ $n=2$ یعنی صفحه، این حکم برقرار است. فضای سهبعدی را در نظر بگیرید، $\mathbb{R}^3$. در زیر یک نمونه میبینید. برابریِ خط آبیِ سمتِ چپ $x=y=1$ و برابریِ خطِ آبیِ سمتِ راست، $x=\frac{y}{2}=1$ است. این دو خط موازی هستند. اکنون خط سبز رنگ با برابریِ $y=\frac{z}{3}=1$ بر خطِ آبیِ سمتِ چپ عمود است ولی بر خط آبی سمت راست عمود نیست. چرا؟ چون اصلا برخوردی ندارند، بلکه دو خطِ متنافر هستند یعنی نه متقاطع و نه موازی.
اکنون آیا این حکم که در $\mathbb{R}^2$ برقرار است، دارای اثبات است؟ بلی. گام نخست این است که گزاره را درست و دقیق بیان کنید.
فرض کنید $\ell_1$ و $\ell_2$ و $\ell_3$ سه خط در $\mathbb{R}^2$ باشند
که $\ell_1$ با $\ell_2$ موازی و $\ell_3$ بر $\ell_1$ عمود باشد. آنگاه
$\ell_3$ بر $\ell_2$ نیز عمود است.
چگونه این را ثابت کنیم؟ خیلی آسان، برابری (معادله) کلیِ این سه خط را بنویسید. سپس شرطهای موازی بودن و عمود بودن آمده در فرض را نیز به شکل برابری (معادله) بنویسید. در آخر ثابت کنید که برابریهایی که تا اینجا دارید با همدیگر، یک برابریِ اضافهتر را نیز نتیجه میدهند که برابریِ مربوط به شرطِ تعامدِ آمده در حکم است. هم میتوانید با محاسبهٔ دستی و صریح این کار را انجام دهید، هم میتوانید از ابزارهای پیشرفتهتر در هندسهٔ جبریِ محاسباتی کمک بگیرید مانند پایههای گروبنر. چون متن پرسشتان تا همین اندازه را میخواهد (دارای اثبات بودن یا نبودن)، بیشتر نمینویسم. ابتدا باید خودتان تلاش کنید و اگر نتوانستید این اثبات را پیاده کنید، در یک پست جدید به همراه (و حتما به همراه) تلاش و محاسباتتان بیاورید تا راهنمایی شوید.