Question

از نقطه M وسط ضلع BC از مثلث ABC بر نیمساز زاویه A عمود کرده ایم تا اضلاع AB و AC یا امتداد انها را به ترتیب در نقاط E و F قطع کند. نشان دهید：CF =BE

Answer 1

$$1. CM=MB\\2.CMF=BME= \beta $$

فرض میکنیم زاویه $ABC$ بزرگتر از زاویه $ACB$ است.

محل برخورد نیمساز و عمود از میانه را $D$ مینامیم.

دو مثلث $ADE$ و$ADF$ بنا بر حالت (ز.ض.ز) همنهشتند، پس:

$$AFD=AED= \alpha $$

از $E$ به مرکزیت $B$ کمانی میزنیم تا نقطه $S$ روی $DE$ بدست آید و $S$ را به $B$ وصل میکنیم تا مثلث متساوی الساقین $BES$ بدست آید، در نتیجه:

$$3.BE=BS$$

$$ESB=BES= \alpha $$

حال داریم

$$FCM=AFD-FMC= \alpha - \beta$$

$$MBS=ESB-EMB= \alpha - \beta $$

در نتیجه:

$$4.FCM=MBS$$

از 1و2و4 بنابر حالت (ز.ض.ز) دو مثلث $BMS$ و $CFM$ هم نهشتند، پس:

$$5.CF=BS$$

از 3 و 5 نتیجه می شود:

$$CF=BE$$

Comments

نقطه D رو کجا گرفتید؟
ضمنا اگر بتونید رسم شکل رو هم بدید ممنون می شم

---

در شکل H نوشتم تویه حل اشتباهی D در نظر گرفتم

ممنون بررسی کردین

الآن درست کنم

---

متاسفانه app برای رسم شکل ندارم

اگه برای گوشی برنامه مناسب معرفی کنین ممنون میشم

---

ممنون از بابت اصلاحتون
نرم افزار geogebra کار دانشگاه برکلی اگه اشتباه نکنم. هم برای رسم در ویندوز و هم در اندرویید نسخه مناسب داره

Answer 2

با توجه به تصویر مقابل:

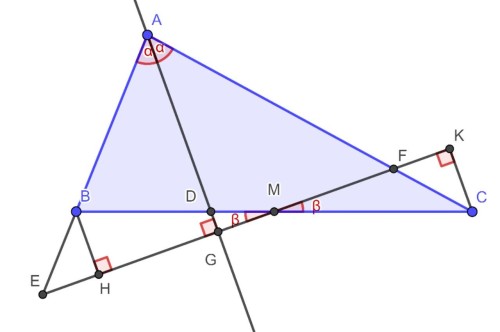
$BM=CM,$

$\angle BMH=\angle CMK=\beta$

بنابراین $\triangle BMH$ و $\triangle CMK$ در حالت (وز) هم نهشتند پس $BH=CK$

بنا به قضیه و اصل خطوط موازی داریم:

$BH\parallel AG\parallel CK\Rightarrow \angle HBE=\angle GAE=\alpha,\angle KCF = \angle GAF=\alpha$

$\Rightarrow \angle HBE=\angle KCF=\alpha,$

$ \angle BHE=\angle CKF=90°,$

$BH=CK$

بنابراین $\triangle BEH$ با $\triangle CFK$ در حالت (زض‌ز) هم نهشتند پس $CF=BE$