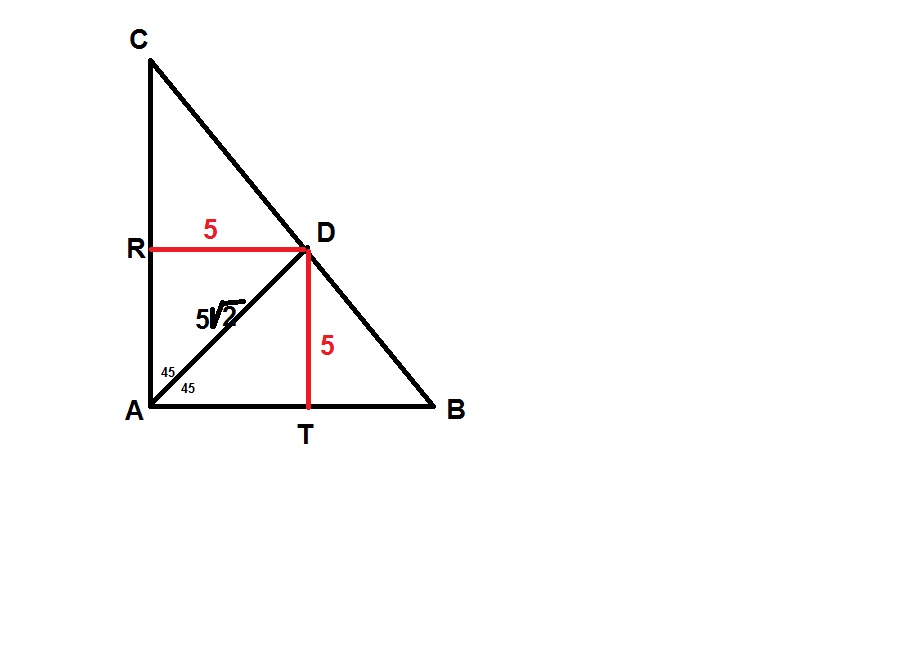
اگرAD نیمساز باشدفاصله نقطه D تا دو ضلع زاویه قائمه به یک اندازه است بنا براین DR=DT که اگر DR رابخواهیم بدست آوریم در مثلثARD داریم $sin45= \frac{DR}{5 \sqrt{2} } = \frac{1}{ \sqrt{2} } $که از این رابطه مقدار DR=5 بدست می آید.همچنین در مثلث ABC طبق قضیه تالس داریم $ \frac{CD}{CB} = \frac{RD}{AB} $ اگر بجای اضلاع حروف کوچکقرار دهیم$ \frac{CD}{a} = \frac{5}{c} $ درنتیجه$ CD= \frac{5a}{c} $ میشود.
طبق خاصیت نیمساز داریم $ \frac{CD}{DB} = \frac{b}{c} $ اگر این رابطه را ترکیب نسبت در مخرج کنیم خواهیم داشت
$\frac{b}{b+c} = \frac{CD}{CD+DB} \Rightarrow \frac{b}{b+c} = \frac{CD}{a} $ اگر CD رااز این رابطه بدست آوریم $CD= \frac{ab}{b+c} $اگر این مقدار را با مقدار قبلی مساوی قرار دهیم داریم:
$ \frac{ab}{b+c} = \frac{5a}{c} $ واگر دو کسر را به a ساده کنیم وسپس هر دو کسر را معکوس کنیم خواهیم داشت:
$ \frac{1}{5} = \frac{b+c}{bc} $ واگر کسرها راتفکیک کنیم $ \frac{c}{bc} + \frac{b}{bc} = \frac{1}{5}$ ودرصورت ساده کردن داریم $ \frac{1}{b} + \frac{1}{c} = \frac{1}{5} $ یعنی مجموع معکوس دو ضلع زاویه قائمه مساوی $ \frac{1}{5} $ است.