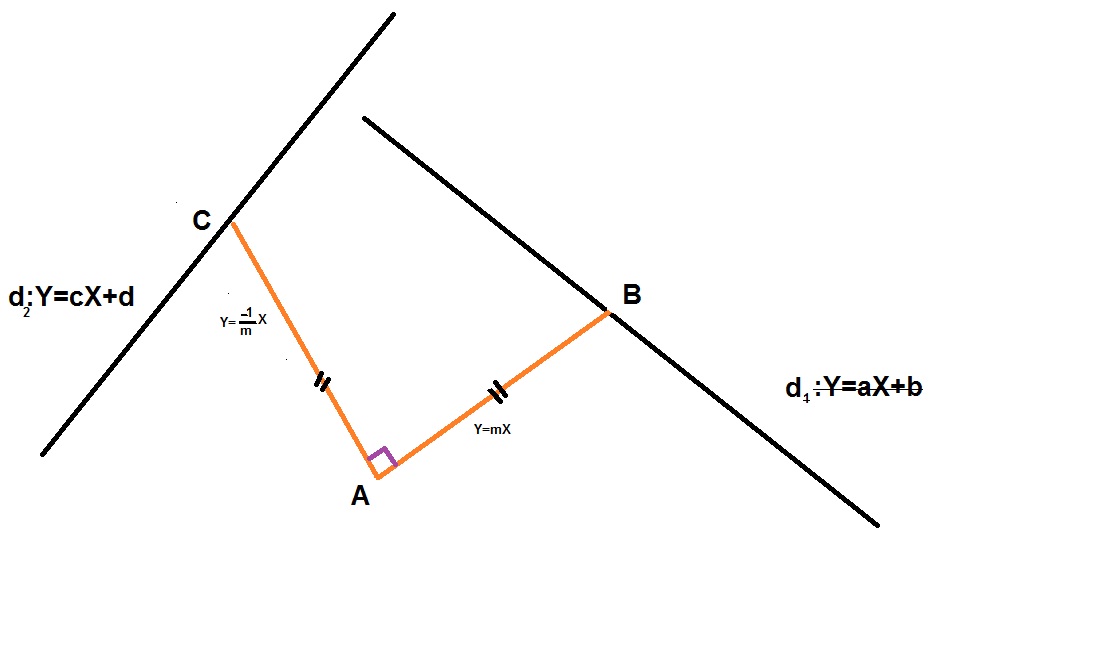
 اگر A مبدا مختصات نباشد با تغییر متغیر$X=x-a و Y=y-b$ که aوb مختصات نقطه Aمیباشد این نقطه به(0و0)تبدیل خواهد شد.همچنین معادله معادلات را در دستگاه جدید بدست می آوریم.این معادلات در شکل نشان داده شده است.
اگر A مبدا مختصات نباشد با تغییر متغیر$X=x-a و Y=y-b$ که aوb مختصات نقطه Aمیباشد این نقطه به(0و0)تبدیل خواهد شد.همچنین معادله معادلات را در دستگاه جدید بدست می آوریم.این معادلات در شکل نشان داده شده است.
دو خطی که از نقطه A رسم شده است چون عمود بر یکدیگرند شیب آنها قرینه وعکس یکدیگرند فرض کنیم یکی از این خطوط خط $ d_{1} $ را در نقطه B و خط دیگر خط $ d_{2} $را در نقطه C قطع کند.
ثابت میکنیم مختصات B وC وابسته به یکدیگرند یعنی طول یکی با قرینه عرض دیگر وعرض یکی با طول دیگر برابر است
فرض کنیم مختصات $B= \begin{bmatrix} \alpha \\ \alpha m \end{bmatrix} $ چون نقطه B روی خط Y=mXنیز میباشد ومختصات نقطه $C= \begin{bmatrix} \beta \\ \frac{-1}{ \ m } \beta \end{bmatrix} $ باشد چون AB=AC می باشد دراین صورت داریم (از فرمول فاصله دو نقطه)
$ \ \alpha ^{2} + \alpha ^{2} m^{2} = \beta ^{2}+ \frac{ \beta ^{2} }{ m^{2} } \Rightarrow \alpha ^{2} (1+ m^{2} )= \beta ^{2} ( \frac{1+ m^{2} }{ m^{2} }) \Rightarrow \beta ^{2} = \alpha ^{2} m^{2} \Rightarrow \beta =
\pm \alpha m $
دلیل اینکه برای $ \beta $دو مقدار بدست میآید این است که دوخط عمود بر هم رسم شده در نقطه A ممکن است که هرکدام هر دو خط را قطع کنند.ا(گر هر خط رسم شده ازA هر دوخط را قطع کند مسئله دو جواب دارد)
بنا بر این مختصات نقطه$C= \begin{bmatrix}- \alpha m \\ \alpha \end{bmatrix} $(رابطه بین مختصات BوC رایاد داشته باشید)
حال شیب دوخط عمود بر هم در نقطه A یعنی مقدار m را بدست می آوریم خط Y=aX+bوخط Y=mX رابا یکدیگر قطع می دهیم تا مختصات نقطهB بر حسب m بدست آیدmX=aX+b در نتیجهX(m-a)=b بنا براین$B= \begin{bmatrix} \frac{b}{m-a} \\ \frac{mb}{m-a} \end{bmatrix} $ ودو خط Y=cX+d وخط$Y= \frac{-1}{m} X$رابا یکدیگر قطع می دهیم
cX+d=$ \frac{-1}{m} X$یعنی طول نقطه C برابر است با$ \frac{-dm}{1+mc} $واین مقدار قرینه عرض نقطه B باید باشدیعنی
$ \frac{-dm}{1+mc} $=$ \frac{-mb}{m-a} $اگر این رابطه را ساده کنیم خواهیم داشت $m= \frac{b+ad}{d-bc} $
در این رابطه مقادیر a,b, c,d ضرایب دوخط داده شده در دستگاه جدید هستند.با بدست آوردن مقدار mمی توان دو خط عمود برهم در نقطه Aرا رسم کرد با این شیب نقا ط تقاطع با دوخط بدست می آید
مثال دوخط Y=2X+1 وY=3X+2داده شده نقاطی از این دوخط پیدا کنید که با مبدا مثلث قائم الزاویه متساوی الساقین درمبدا قائمه بسازند .
حل : $m= \frac{1+4}{2-3} $ با این شیب نقاط $B= \begin{bmatrix} \frac{-1}{7} \\ \frac{5}{7} \end{bmatrix} $
ونقطه $C= \begin{bmatrix} \frac{-5}{7} \\ \frac{-1}{7} \end{bmatrix} $ بدست میآید طبق آنچه گفته شده شیب بدست آمده را اگر در خطوط عوض کنیم دو نقطه دیگر نیز بدست میآید.
اگر طریقه رسم برای پیدا کردن دو نقطهB و C راخواسته باشند ومختصات نقاط را نخواسته باشیم بعد از آن که نقطهAوخطوط را در دستگاه جدید بدست آوردیم باتوجه به تعریف شیب m که عرض تقسیم به طول است $m= \frac{b+ad}{d-bc} $
ازنقطه A به اندازه d-bc افقی حرکت میکنیم اگر این مقدار مثبت بود بطرف راست واگر منفی بود بطرف چپ سپس به اندازه
b+ad بطرف بالا (اگر مثبت بود)یا بطرف پایین اگر منفی بود حرکت می کنیم نقطه انتها را به A وصل کرده وامتداد میدهیم تا خط های داده را قطع کند سپس از نقطه Aیک عمودبر این خط اخراج می کنیم تا خطهای داده شده را قطع کند محل تلاقی جواب مسئله است.