اگر زاویه$ \theta $ به طورمثال $ \theta =60^{ \circ } $ داشته باشیم باتوجه به شکل زوایای CBD و CED مکملند بااستفاده از قضیه کسینوس ها ابتدا x برحسب $ \theta $ وسپس a رابرحسب $ \theta $ به دست می آوریم و مسئله قابل رسم است 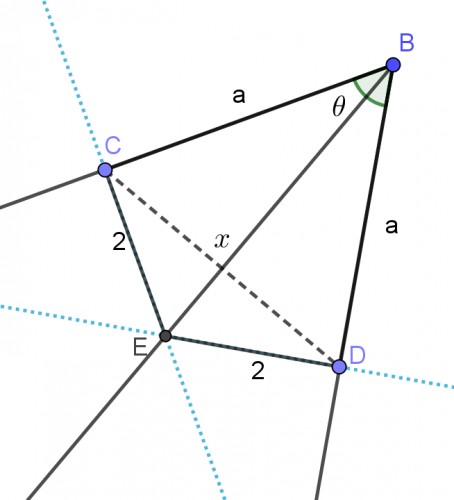
$x^2 =8-2\times 2 \times 2cos(180-60)=8+4=12$ ودرمثلث CBD
<$12=2a^2-2a^2 \times cos60$>
درنتیجه $a= \sqrt[]{12} $ به این ترتیب با این مثال از نقطه B بامعلوم شدن a از نقاط CوD با رسم عمود
CE و DE را به اندازه 2 سانتی متر رسم کنیم نقطه تلاقی آنها نقطه مطلوب روی نیمساز خواهد بود.این را می توان به طورکلی با هر مقدار $ \theta $ نیز نوشت.
$ a= \sqrt[]{\frac{4(1+cos\theta) }{1-cos \theta}}= \frac{2 sin\theta}{1-cos \theta} $