چون $ABC$ متساوی الاضلاع است لذا $B \hat{A}C=A\hat BC=A\hat CB=60 $. لذا در مثلث متساوی الساقین $BCD$داریم: $D\hat BC=120$ و $B\hat DC= B\hat CD=30 $. بنابراین $ A\hat CG=90$یعنی مثلث $ACG$ قائم الزاویه است. اگر از $G$ عمود $GI$ را بر $CH$ وارد کنیم داریم: $G\hat CI=30$. اگر قرار دهیم $x=AG$ در اینصورت با استفاده از تعریف سینوس این زاویه خواهیم داشت $GI=\frac12CG=\frac12\sqrt{1-AG^2}$.
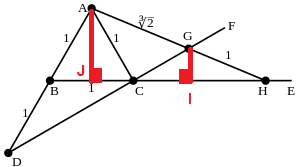
از طرفی $AJ$ عمود بر $BC$ از وسط $BC$ می گذرد چون مثلث $ABC$ متساوی الاضلاع است. لذا با قضیه فیثاغورث داریم
$AJ=\frac{\sqrt 3} 2$. اما مثلث های $GIH$و $AJH$ با هم متشابهند(چون تمام زوایای نظیر به نظیر برابرند) لذا: $$\frac{GI}{AJ}=\frac{GH}{AH}$$ با جاگذاری داریم:
$$\frac12\sqrt{x^2-1}=\frac{\sqrt3}2\frac{1}{x+1}$$
بعد از ساده کردن این عبارت خواهیم داشت: $ x^4+2x^3-2x-4=0 $. اما $x=-2$ یکی از ریشه های این معادله است. بعد از تجزیه کردن خواهیم داشت: $x^4+2x^3-2x-4=(x+2)(x^3-2)$. بنابراین یا $x=-2$که غیر قابل قبول است چون طول ضلع نمی تواند منفی باشد و یا $x^3-2=0$یعنی $x=\sqrt[3]2$.
راهنمایی و روش دیگر http://www.numbersandshapes.net/?p=2664