از آنجا که سوال شما در مورد کتاب حساب دیفراننسیل انتگرال پیش دانشگاهی است خوب است که به کتاب حساب دیفرانسیل بخش رسم توابع رجوع کنید در آنجا چندین مثال به خوبی توضیح داده شده است.
از جمله موارد مهمی که برای رسم توابع می توانیم از آنها کمک بگیریم عبارت اند از:
- دامنه تابع
- تقارن و یا متناوب بودن: زوج و فرد بودن
- نقاط برخورد با محورهای مختصات
- مجانب های قائم، افقی و مایل در صورت وجود
- صعودی نزولی بودن تابع و نقاط اکسترمم نسبی و مطلق: می توانیم از مشتق برای این مطلب کمک بگیریم
- تقعرو نقاط عطف تابع : می توانیم از مشتق مرتبه دوم استفاده کنیم
- تنظیم جدول تغییرات
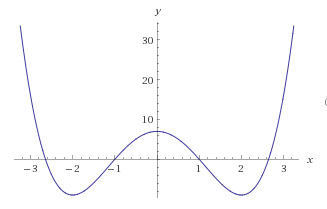
به عنوان مثال برای رسم تابع $f(x)=x^4-8x^2+7$ به صورت زیر عمل میکنیم:
دامنه تابع برابر کل اعداد حقیقی است چون تابع چندجمله ای است: $D_f=\mathbb R$
این تابع زوج است (چرا؟) لذا کافی است آن را فقط برای $x\geq 0$ رسم کنیم و با استفاده از تقارن برای $x< 0$ آن را رسم کنیم.
با قرار دادن $x=0$ میتوانید محل برخورد با محور $y$ ها را بیابید:
$$x=0\Rightarrow f(x)=7$$
لذا $(0,7)$ یک نقطه از نمودار است.
همچنین با قرار دادن $y=0$ می توان نقاط برخورد با محور $x$ها را بیابید:
$$x^4-8x^2+7=0\Rightarrow (x^2-1)(x^2-7)=0\Rightarrow \begin{cases}x=\pm 1\\ x=\pm \sqrt 7\end{cases}$$
پس $(\pm 1,0),(\pm\sqrt7,0)$ روی نمودار تابع قرار دارند.
این تابع هیچ مجانبی ندارد (چرا؟)
با مشتق گیری داریم:
$f'(x)=4x^3-16x=0\Rightarrow \begin{cases}x=0\\x=\pm 2\end{cases}$
و از مشتق دوم داریم:
$f''(x)=12x^2-16=0\Rightarrow x=\pm\sqrt{\frac43}=\pm \frac{2}{\sqrt 3}=\pm \frac{2\sqrt3}{3}$
می توانیم جدول تغییرات را برای $f'$ و $f''$ در یک جدول و یا جداگانه برای هر کدام تنظیم کنیم:
$$
\begin{array}{c|lccccccr}
x& -\infty& & -2& & 0& &2& &+\infty\\
\hline
f'(x)& &-&0&+&0 & - &0 &+ \\
\hline
f(x)& +\infty& \searrow &-9 & \nearrow & 7& \searrow &-9 & \nearrow&+\infty \\
\end{array}
$$
$$
\begin{array}{c|lcccr}
x& -\infty& & -\frac{2\sqrt3}{3}& &\frac{2\sqrt3}{3}& &+\infty\\
\hline
f''(x)& & +& 0&- & 0& +\\
\hline
f(x)&+\infty & \smile &-\frac{-17}{9} & \frown &-\frac{17}9 & \smile &+\infty
\end{array}
$$
با توجه به جدول تغییرات میفهمیم که تابع در بازه $(-\infty, -2]$ اکیدا نزولی است. در $[-2,0]$ اکیدا صعودی در $[0,2]$ اکیدا نزولی و در $[2,+\infty)$ اکیدا صعودی است. پس کافی است بعد از مشخص کردن نقاط $(-2,-9),(0,7),(2,-9)$ روی نمودار سعی کنید که با توجه به صعودی نزولی بودن تابع در بازه های گفته شده تابعی رسم کنید که شرایط گفته شده را برقرار کند. همچنین چون در جدول تغییرات تابع در سمت چپ و راست نقطه های $-2,2$ تابع به صورت $ \searrow \nearrow $ پس این نقطه یک نقطه ی مینیمم نسبی است و چون در نقطه ی $0$ به صورت $ \nearrow \searrow $ لذا صفر یک نقطه ی ماکسیمم نسبی است. در حین رسم باید به این نکته ی مهم توجه بکنید که جهت تقعر تابع در
$(-\infty, -\frac{2\sqrt3}3)$ رو به بالا و در $(-\frac{2\sqrt3}{3},\frac{2\sqrt3}{3})$ رو به پایین و در
$(\frac{2\sqrt3}{3},+\infty)$ رو به بالا است.
خلاصه شما با توجه به جدول تغییرات نمودار نقاط پیدا شده را به همدیگر وصل میکنید به طوریکه با نگاه کردن به نمودار تابع بتوان جدول تغییرات تابع را حدس زد. و بعد از تمرین کردن و حل چند مساله اگر واقعا بتوانید تمام موارد گفته شده را بیابید رسم نمودار آن خیلی دشوار نخواهد بود!
می توانید در اینجا نمودار تابع بالا را ببینید: