دامنه ی تابع در حالت کلی $\mathbb R$ است ولی آن را محدود کرده و در $[\frac{\pi}2,\frac{5\pi}2]$ در نظر گرفته است.
برای پیدا کردن محل برخورد با محور $y$ ها باید قرار دهیم $x=0$ ولی چون صفر عضوی از دامنه نیست پس نیازی به این کار نیست.
برای پیدا کردن محل برخورد با محور $x$ ها باید معادله ی $\cos^2 x-\cos x=0$ حل شود که داریم:
$$\begin{cases}\cos x=0\Rightarrow x= \frac\pi2, \frac{3\pi}2, 2\pi+\frac\pi2\\
\cos x=1\Rightarrow x=2\pi\end{cases}$$
اگر از آن مشتق بگیریم داریم: $y'=-2\sin x\cos x+\sin x=0$ داریم $\sin x=0$ یا
$\cos x=\frac 12$ و در بازه ی مذکور جواب این معادلات به ترتیب برابر
$$ \begin{cases}\sin x=0\Rightarrow x=\pi, 2\pi \\
\cos x=\frac12 \Rightarrow x=2\pi\pm \frac\pi3
\end{cases} $$
در اینصورت با جاگذاری موارد بالا در جدول داریم:
$$\begin{array}{c|lcccccccr}
x&\frac\pi2 & &\pi& &2\pi-\frac\pi3& &2\pi& &2\pi+\frac\pi3& &\frac{5\pi}2\\
\hline
sinx& &+& 0&-&-& -&0&+&+&+&\\
\hline
1-\\ 2cosx&&+&+&+&0&-&-&-&0&+\\
\hline
y'& &+&0&-&0&+&0&-&0&+\\
\hline
y&0&\nearrow&2&\searrow &-\frac12 &\nearrow&-\frac12 &\searrow&0&\nearrow&0\end{array}$$
چون در سمت چپ و راست نقطه ی $\pi$ به صورت $ \nearrow \searrow $ است لذا این نقطه ماکسیمم نسبی است و به همین ترتیب نقطه ی $2\pi-\frac\pi3$ مینیمم نسبی و $2\pi$ ماکسیمم نسبی و $2\pi+\frac\pi3$ مینیمم نسبی است. با یافتن نقاط بالا داریم:
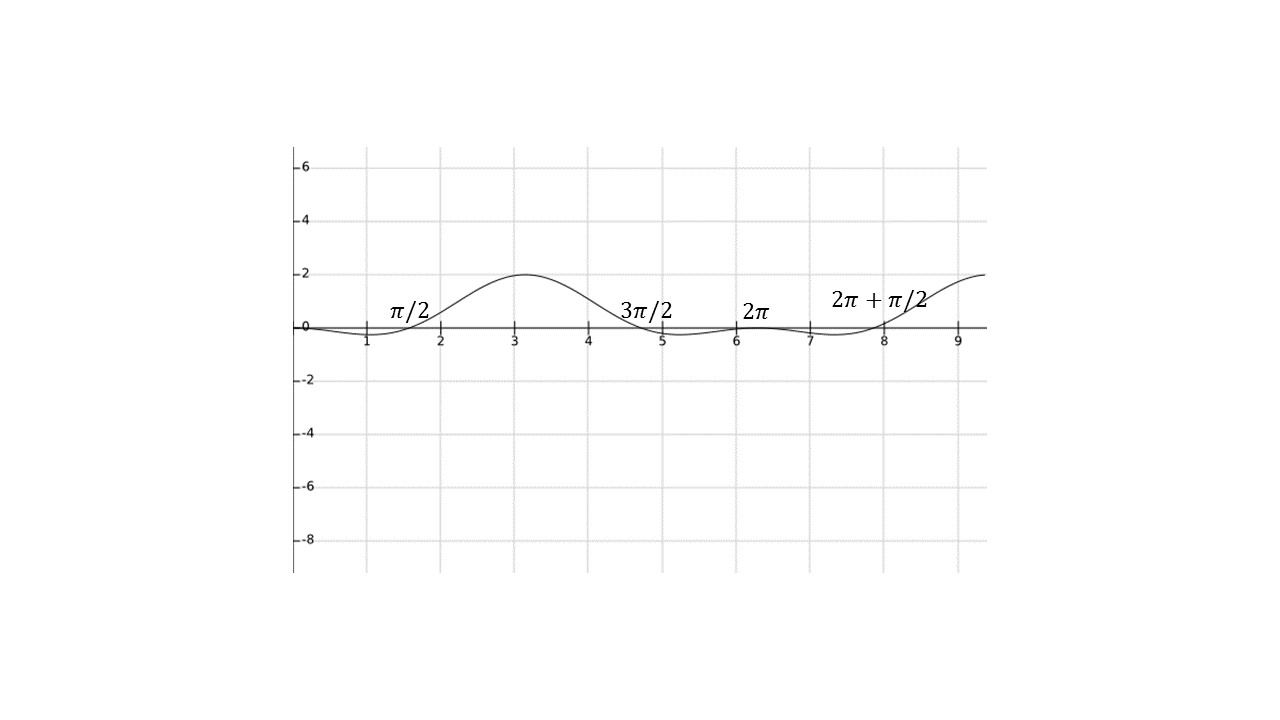
رسم شکل در wolframalpha و fooplot