یک نمودار ون مانند زیر بکشید.
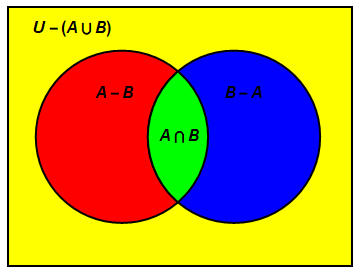
برای افرادی که علاقهمند هستند دستور کشیدن این شکل بوسیلهٔ نرمافزار Mathematica نیز در انتهای پاسخ گذاشتهشدهاست. چه کاری کردهایم در این شکل؟ کل فضا را به مجموعههای بدون اشتراک تفکیک کردهایم. یعنی ۴ مجموعه نمایش دادهایم که هیچ دو تای آنها اشتراک ناتهی ندارند. این چهار مجموعه عبارت اند از؛ $A-B$ و $B-A$ و $A\cap B$ و $U-(A\cup B)$. به این کار اصطلاحا افرازکردن میگویند یعنی مجموعهای را به شکل اجتماع زیرمجموعههای دو به دو مجزایشان نوشتن. در اینجا ما مجموعهٔ مرجع شما یعنی $U$ را نسبت به $A$ و $B$ با فرض اینکه نمیدانیم تعداد اعضای هر قسمت چند است افراز کردیم (اگر میدانستیم که مثلا یکی از این چهار قسمت تهی است، آن را در افراز نمیآوریم). دو داده دارید $|(A\cap B)^c|=11$ و $|A^c|+|B|=13$. دقت کنید که به جای نمادهای شما از نمادهای $|.|$ و $.^c$ برای عدد اصلی (تعداد اعضا) و متمم یک مجموعه استفاده کردهایم. برای حل توجه کنید که چون چهار قسمت معرفی شده بوسیلهٔ ما مجزا هستند پس تعداد اعضای هر یک مستقل است و عضوی در دو تای آنها تکرار نمیشود پس چهار مجهول معرفی میکنیم.
$$\begin{array}{ll}
|A-B| &= x_1\\
|B-A| &= x_2\\
|A\cap B| &= x_3\\
|(A\cup B)^c| &=x_4
\end{array}$$
دقت کنید که $(A\cap B)^c=(A-B)\cup (B-A)\cup (A\cup B)^c$ پس دادهٔ نخست شما این برابری را میدهد؛
$$x_1+x_2+x_4=11$$
بعلاوه توجه کنید که $A^c=(B-A)\cup(A\cup B)^c$ و $B=(B-A)\cup(A\cap B)$ پس دادهٔ دوم شما این برابری را میدهد؛
$$(x_2+x_4)+(x_2+x_3)=13$$
پس شما یک دستگاه دو معادله چهار مجهولی به شکل زیر دارید که فرضهای شما میگوید مقادیر مجهولها باید در این دستگاه خطی صدق کند.
$$\left\lbrace\begin{array}{lllll}
x_1+ & x_2+ & & x_4 & =11\\
& 2x_2+ & x_3+ & x_4 & =13
\end{array}\right.$$
اکنون چیزی که شما دنبالش هستید چیست؟ توجه کنید که چون $A\cup B^c=(A-B)\cup (A\cap B)\cup (A\cup B)^c$ پس $|A\cup B^c|=x_1+x_3+x_4$ که این جمع در فضای برداری تولید شده بوسیلهٔ سمت چپهای دو برابری دستگاه خطیتان نیست. به زبان سادهتر بوسیلهٔ دو برابریِ دادهشدهتان نمیتوانید حاصلِ $x_1+x_3+x_4$ را یافت (این پرسش پاسخِ یکتا ندارد). برای نمونه برای هر دو عدد طبیعی دلخواه که دو عبارتِ زیر را منفی نکنند برای $x_2$ و $x_4$ کافی است قرار دهید
$$\begin{array}{l}
x_1=11-(x_2+x_4)\\
x_3=13-(2x_2+x_4)
\end{array}$$
آنگاه یکی از چندین حالت ممکن را یافتهاید. برای نمونه دو حالت ممکن را در زیر میآوریم.
$$\begin{array}{l}
x_2=x_4=1 \Longrightarrow x_1=9,\;x_3=10\\
x_2=2,\;x_4=5 \Longrightarrow x_1=4,\;x_3=4
\end{array}$$
البته تعداد حالتهای ممکن به خاطر عدد طبیعی بودن تعداد اعضای این مجموعهها متناهی خواهد بود که در صورت داشتن علاقه میتوانید به تعداد پاسخها فکر کنید.
rectangle=Graphics[{EdgeForm[Thick],Yellow,Rectangle[{0,-1.5},{4,1.5}]}];
circle1=Graphics[{EdgeForm[Thick],Red,Disk[{1.325,0},1]}];
circle2=Graphics[{EdgeForm[Thick],Blue,Disk[{2.625,0},1]}];
intersection=RegionIntersection[Disk[{1.325,0},1],Disk[{2.625,0},1]];
intersectionPlot=Region[Style[intersection,Green,EdgeForm[Directive[Thick,Black]]]];
text1=Graphics[Text[Style[ToExpression["U-(A\\cup B)",TeXForm,HoldForm],FontSize->16,Bold],{0.75,1.25}]];
text2=Graphics[Text[Style[ToExpression["A",TeXForm,HoldForm],FontSize->16,Bold],{1.25,0.5}]];
text3=Graphics[Text[Style[ToExpression["B",TeXForm,HoldForm],FontSize->16,Bold],{2.75,0.5}]];
text4=Graphics[Text[Style[ToExpression["A\\cap B",TeXForm,HoldForm],FontSize->16,Bold],{2,0}]];
Show[rectangle,circle1,circle2,intersectionPlot,text1,text2,text3,text4]