Ш§ЫҢЩҶ ЩҫШұШіШҙ ЩҲ ЩҶЩ…ЩҲЩҶЩҮвҖҢЩҮШ§ЫҢ Щ…ШҙШ§ШЁЩҮвҖҢШҙШ§ЩҶ ШіШ§ШҜЩҮ ЩҮШіШӘЩҶШҜ. ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ ЪҶЫҢШІЫҢ Ъ©ЩҮ ШҜЩҶШЁШ§Щ„Шҙ ЩҮШіШӘЫҢШҜ ШұШ§ Ш§ЫҢЩҶ ЪҜЩҲЩҶЩҮ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶЫҢШҜ ШЁШ§ШІЪҜЩҲЫҢЫҢ Ъ©ЩҶЫҢШҜ. ЫҢЪ© ЩҶЩӮШ·ЩҮЩ” Ш«Ш§ШЁШӘ ШҜШ§ШұЫҢШҜ $A$ШҢ ЩҲ ЫҢЪ© Щ…Ш¬Щ…ЩҲШ№ЩҮ (Щ…ЫҢвҖҢШӘЩҲШ§ЩҶЫҢШҜ ЩҮШұ ЪҶЫҢШІЫҢ ШӯШӘЫҢ ЩҶШ§ШұЩҲЫҢЩҮ ШЁШ§ШҙШҜ) $S$. Ш§ЫҢЩҶ ШҜЩҲ ШҙЫҢШЎ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶЩҶШҜ ШҜШұ ЩҒШ¶Ш§ЫҢЫҢ ШЁШ§ ШЁШ№ШҜ ШҜЩ„Ш®ЩҲШ§ЩҮ ШЁШ§ШҙЩҶШҜ ЩҲ ЩҒЩӮШ· ШЁЩҮ Ыі ШЁШ№ШҜ Щ…ШӯШҜЩҲШҜ ЩҶЫҢШіШӘ. ШҜШұ Щ…Ш«Ш§Щ„ ШҙЩ…Ш§ Ыі ШЁШ№ШҜЫҢ ЩҮШіШӘЩҶШҜ. ШҜШ§ШұЫҢЩ… $A=(0,0,0)$ ЩҲ $S=\lbrace (x,y,z,)\in\mathbb{R}^3\mid z^2-xy-1=0\rbrace$. ЩҒШұШ¶ Ъ©ЩҶЫҢШҜ $(x,y,z)$ ЫҢЪ© ЩҶЩӮШ·ЩҮ ШҜШұ $S$ ШЁШ§ШҙШҜШҢ ЩҒШ§ШөЩ„ЩҮЩ” Ш§ЫҢЩҶ ЩҶЩӮШ·ЩҮ Ш§ШІ $A$ Щ…ЫҢвҖҢШҙЩҲШҜ
$$\sqrt{(x-x_A)^2+(y-y_A)^2+(z-z_A)^2}$$
Ш§Ъ©ЩҶЩҲЩҶ ШҙЩ…Ш§ Щ…ЫҢвҖҢШ®ЩҲШ§ЩҮЫҢШҜ ЩҫШұШіШҙ ШЁЩҮЫҢЩҶЩҮвҖҢШіШ§ШІЫҢ ШІЫҢШұ ШұШ§ ШӯЩ„ Ъ©ЩҶЫҢШҜ.
$$\min(\sqrt{(x-x_A)^2+(y-y_A)^2+(z-z_A)^2})\;\text{ s.t. }\;(x,y,z)\in S$$
ЫҢШ№ЩҶЫҢ ЫҢШ§ЩҒШӘЩҶ Ъ©Щ…ЫҢЩҶЩҮЩ” ШӘШ§ШЁШ№ ШіЩҮвҖҢЩ…ШӘШәЫҢШұЩҮЩ” ШЁШ§Щ„Ш§ Ъ©ЩҮ $x_A$ ЩҲ $y_A$ ЩҲ $z_A$ Ш«Ш§ШЁШӘ ЩҮШіШӘЩҶШҜ ЩҲЩ„ЫҢ $x$ ЩҲ $y$ ЩҲ $z$ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶЩҶШҜ ШЁШұ ШұЩҲЫҢ $S$ ШӘШәЫҢЫҢШұ Ъ©ЩҶЩҶШҜ. ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ ШӘШ§ШЁШ№ЫҢ Ъ©ЩҮ Щ…ЫҢвҖҢШ®ЩҲШ§ЩҮЫҢЩ… Ъ©Щ…ЫҢЩҶЩҮ Ъ©ЩҶЫҢЩ… ШІЩ…Ш§ЩҶЫҢ Ъ©Щ…ЫҢЩҶЩҮ Щ…ЫҢвҖҢШҙЩҲШҜ Ъ©ЩҮ ШЁШҜЩҲЩҶ Ш¬Ш°ШұШҙ Ъ©Щ…ЫҢЩҶЩҮ ШҙЩҲШҜ (ШІЫҢШұ Ш¬Ш°Шұ ЩҶШ§Щ…ЩҶЩҒЫҢ Ш§ШіШӘ). ЩҲ Ш§ЫҢЩҶ ЩҶЪ©ШӘЩҮ ШЁЩҮ ШҙЪ©Щ„ Ш§ЪҜШұ ЩҲ ШӘЩҶЩҮШ§ Ш§ЪҜШұ Ш§ШіШӘ. ЩҫШі ШҜШұ ЩҫШұШіШҙ ШҙЩ…Ш§ ЩҮШҜЩҒ ШЁЩҮ ШҙЪ©Щ„ ШІЫҢШұ ШЁШ§ШІЩҶЩҲЫҢШіЫҢ Щ…ЫҢвҖҢШҙЩҲШҜ.
$$\min(x^2+y^2+z^2)\;\text{ s.t. }\;z^2-xy-1=0$$
Ш§Ъ©ЩҶЩҲЩҶ ШЁШ§ЫҢШҜ ШЁЩҮ ЫҢШ§ШҜ ЪҶЫҢШІЫҢ Ш§ЩҒШӘШ§ШҜЩҮ ШЁШ§ШҙЫҢШҜ! Ш¶ШұЫҢШЁвҖҢЩҮШ§ЫҢ Щ„Ш§ЪҜШұШ§ЩҶЪҳ. ШҜШұ ЩҮЩ…ЫҢЩҶ ШіШ§ЫҢШӘ ШӘШ№ШҜШ§ШҜ ШІЫҢШ§ШҜЫҢ ЩҫШіШӘ ЩҫЫҢШұШ§Щ…ЩҲЩҶ Ш¶ШұЫҢШЁвҖҢЩҮШ§ЫҢ Щ„Ш§ЪҜШұШ§ЩҶЪҳ ЩҮШіШӘ ЩҫШі ШЁШҜЩҲЩҶ Щ…ЩӮШҜЩ…ЩҮ ШіШұШ§Шә ШҜЩҶШЁШ§Щ„ЩҮЩ” ШӯЩ„ Щ…ЫҢвҖҢШұЩҲЫҢЩ…. ЫҢЪ© Щ…ШӘШәЫҢШұ Ъ©Щ…Ъ©ЫҢ Щ…ЫҢвҖҢШ§ЩҒШІШ§ШҰЫҢЩ… ЩҲ ШӘШ§ШЁШ№ Ш¬ШҜЫҢШҜ $H$ ШІЫҢШұ ШұШ§ ШӘШ№ШұЫҢЩҒ Щ…ЫҢвҖҢЪ©ЩҶЫҢЩ….
$$H(x,y,z)=(x^2+y^2+z^2)+\lambda(z^2-xy-1)$$
ЩҶЩӮШ·ЩҮвҖҢШ§ЫҢ Ъ©ЩҮ Ъ©Щ…ЫҢЩҶЩҮЩ” ШҙЩ…Ш§ ШҜШұ ШўЩҶ ШұШ® Ш®ЩҲШ§ЩҮШҜ ШҜШ§ШҜ Ш¬ШІЩҲ ЩҶЩӮШ·ЩҮвҖҢЩҮШ§ЫҢ ШЁШӯШұШ§ЩҶЫҢ Ш§ЫҢЩҶ ШӘШ§ШЁШ№ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ. ЩҫШі ШҜШіШӘЪҜШ§ЩҮ Щ…ШҙШӘЩӮвҖҢЩҮШ§ЫҢ ЩҫШ§ШұЩҮвҖҢШ§ЫҢ (Ш¬ШұШҰЫҢ) ШұШ§ ШӘШҙЪ©ЫҢЩ„ ЩҲ ШӯЩ„ Щ…ЫҢвҖҢЪ©ЩҶЫҢЩ…. $\frac{\partial H}{\partial x}=\frac{\partial H}{\partial y}=\frac{\partial H}{\partial z}=\frac{\partial H}{\partial \lambda}=0$. Ш§ЫҢЩҶ ШҜШіШӘЪҜШ§ЩҮ ШҜШ§ШұШ§ЫҢ ЪҶЩҮШ§Шұ ЩҫШ§ШіШ® ШӯЩӮЫҢЩӮЫҢ Ш§ШіШӘ. Ш§ЫҢЩҶ ЪҶЩҮШ§Шұ ЩҶЩӮШ·ЩҮ ШұШ§ ШҜШұ ШӘШ§ШЁШ№ ЩҒШ§ШөЩ„ЩҮЩ” Ш§ШөЩ„ЫҢ Щ…ЫҢвҖҢЪҜШ°Ш§ШұЫҢЩ…. ШҜЩҲШӘШ§ Ш§ШІ ШўЩҶЩҮШ§ Щ…ЩӮШҜШ§Шұ Ыұ ЩҲ ШҜЩҲШӘШ§ЫҢ ШҜЫҢЪҜШұ Щ…ЩӮШҜШ§Шұ $\sqrt{2}$ ШұШ§ Щ…ЫҢвҖҢШҜЩҮЩҶШҜ. ЩҫШі Ъ©Щ…ШӘШұЫҢЩҶ ЩҒШ§ШөЩ„ЩҮЩ” Щ…Щ…Ъ©ЩҶ ШЁШұШ§ШЁШұ ШЁШ§ Ыұ Ш§ШіШӘ ЩҲ ШҜШұ ШҜЩӮЫҢЩӮШ§ ШҜЩҲ ЩҶЩӮШ·ЩҮ ШұЩҸШ® Щ…ЫҢвҖҢШҜЩҮШҜШҢ ЩҶЩӮШ·ЩҮвҖҢЩҮШ§ЫҢ $(0,0,1)$ ЩҲ $(0,0,-1)$. ШҜШұ ШІЫҢШұ Щ…ШӯШ§ШіШЁЩҮвҖҢЩҮШ§ ШЁШ§ Ъ©Щ…Ъ© ЩҶШұЩ…вҖҢШ§ЩҒШІШ§Шұ Maple ШўЩҲШұШҜЩҮ ШҙШҜЩҮвҖҢШ§ЩҶШҜ. Ш§Щ„ШЁШӘЩҮ Ш§ЫҢЩҶ Щ…ШӯШіШ§ШЁЩҮвҖҢЩҮШ§ ШЁШ§ ШҜШіШӘ ЩҶЫҢШІ ШЁЩҮ ШіШ§ШҜЪҜЫҢ Ш§ЩҶШ¬Ш§Щ… Щ…ЫҢвҖҢШҙШҜЩҶШҜ. ШЁШ№Щ„Ш§ЩҲЩҮ ШұШіЩ… ЫҢЪ© ШҙЪ©Щ„ ЩҶЫҢШІ Ш§ЩҒШІЩҲШҜЩҮвҖҢШҙШҜЩҮвҖҢШ§ШіШӘ.
H:=((x-0)^2+(y-0)^2+(z-0)^2)+lambda*(z^2-x*y-1);
F:=[seq(diff(H,j)=0,j in [x,y,z,lambda])];
sols:=[solve(F,{x,y,z,lambda},real)];
for j in sols do
eval((x-0)^2+(y-0)^2+(z-0)^2,j);
end do;
pPoints:=plots:-pointplot3d([[0,0,0],[0,0,-1],[0,0,1],[1,-1,0],[-1,1,0]],color=[yellow,blue,blue,red,red],symbol=solidsphere,symbolsize=20):
pSurface:=plots:-implicitplot3d(z^2-x*y-1=0,x=-2..2,y=-2..2,z=-2..2,style=surface,color=cyan,transparency=0.5):
plots:-display(pPoints,pSurface,scaling=constrained,view=[-2..2,-2..2,-2..2]);
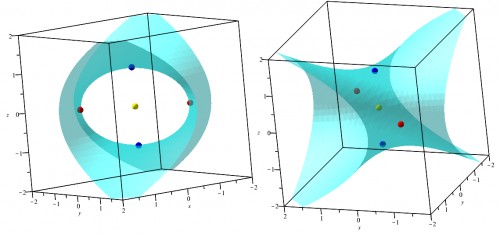
ШҙЪ©Щ„ Щ…ЩҲШұШҜ ЩҶШёШұ ШҜШұ ШІЫҢШұ ШўЩ…ШҜЩҮвҖҢШ§ШіШӘ. ЩҶЩӮШ·ЩҮЩ” $A$ ШЁЩҮ ШұЩҶЪҜ ШІШұШҜШҢ ШұЩҲЫҢЩҮЩ” Щ…ЩҲШұШҜ ЩҶШёШұ ШЁШ§ ШұЩҶЪҜ ШўШЁЫҢ ШўШіЩ…Ш§ЩҶЫҢ ЩҲ ШЁШ§ ШӯШ§Щ„ШӘ ЩҶЫҢЩ…ЩҮвҖҢШҙЩҒШ§ЩҒШҢ ЩҶЩӮШ·ЩҮвҖҢЩҮШ§ЫҢЫҢ Ъ©ЩҮ Ъ©Щ…ЫҢЩҶЩҮ ШҜШұ ШўЩҶЩҮШ§ ШұШ® Щ…ЫҢвҖҢШҜЩҮШҜ ШЁШ§ ШўШЁЫҢ ЩҲ ШҜЩҲ ЩҶЩӮШ·ЩҮЩ” Ш§Ш¶Ш§ЩҒЩҮ ШЁШ§ ШұЩҶЪҜ ЩӮШұЩ…ШІ ЩҶЩ…Ш§ЫҢШҙ ШҜШ§ШҜЩҮвҖҢШҙШҜЩҮвҖҢШ§ЩҶШҜ.