پرسش را به امان خدا رها کردن و دست به مداد نشدن هیچگاه پرسش را حل نمیکند. پرسش گفتهاست با رسم نمودار، تا به حال هیچ نموداری نکشیدهاید؟ برای نمونه در پایههای پیشین کشیدنِ نمودارِ $y=x+2$ یا $y=x^2$ و غیره نداشتید؟ چه کار میکردید، اولین چیزی که یاد گرفتید این بود که یک سری مقدار برای $x$ بردارید مثلا $x=0$ و $x=1$ و غیره، در ضابطهٔ تابع جایگذاری کنید، سپس نقطههای $(x,y)$ای که بدست آوردید را بر روی صفحهٔ مختصات مشخص میکردید و در آخر اینها را صاف یا خمدار به هم وصل میکردید، نه؟ آیا همچین کاری اینجا کردید؟ به احتمال خیلی زیاد اصلا!
بیایید مقدارهای $\lbrace -4,-2,-1,-\frac{1}{2},-\frac{1}{4},\frac{1}{4},\frac{1}{2},1,2,4\rbrace$ را برای $x$ در هر دو حالتِ $y=\frac{1}{x}$ و $y=\frac{1}{x^2}$ جایگذاری کنیم. جدولهای زیر را خواهیم داشت.
$$\begin{array}{l|llllllllll}
x & -4 & -2 & -1 & -\frac{1}{2} & -\frac{1}{4} & \frac{1}{4} & \frac{1}{2} & 1 & 2 & 4\\\hline
\frac{1}{x} & -\frac{1}{4} & -\frac{1}{2} & -1 & -2 & -4 & 4 & 2 & 1 & \frac{1}{2} & \frac{1}{4}
\end{array}$$
توجه کنید که مقدارِ صفر را انتخاب نکردیم چون جزو دامنهٔ تابعهایمان نیست. برای تابع یکُم این نقطهها و وصلشدهشان به شکلِ زیر میشود.
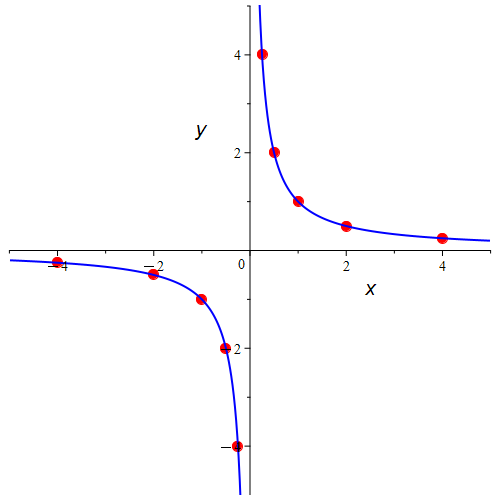
آیا انتخاب مقدارهای $x$ باید دقیقا همان عددهای جدول ما باشد؟ خیر، شما میتوانید عددهای دیگری را انتخاب کنید. ولی باید یک سری عدد پیش از صفر و یک سری عدد پس از صفر را داشته باشد چون قرار است پیرامون حد داشتن و مقدارش در $x=0$ قضاوت کنید پس باید بدانید که رفتارِ تابع در حول و حوش این مقدار چگونه است.
به هر حال با توجه به شکل نتیجه پیرامون حد تابع زمانی که $x$ به صفر میل میکند این است که حد وجود ندارد، چرا؟ چون از سمتِ چپ تابع به منفی بینهایت میل میکند ولی از سمت راست به مثبت بینهایت و چون حد چپ و راست برابر نیست، تابع در این نقطه حد ندارد.
برای تابع دوم جدول زیر را داریم.
$$\begin{array}{l|llllllllll}
x & -4 & -2 & -1 & -\frac{1}{2} & -\frac{1}{4} & \frac{1}{4} & \frac{1}{2} & 1 & 2 & 4\\\hline
\frac{1}{x^2} & \frac{1}{16} & \frac{1}{4} & 1 & 4 & 16 & 16 & 4 & 1 & \frac{1}{4} & \frac{1}{16}
\end{array}$$
نمودار برای این تابع به شکل زیر میشود.
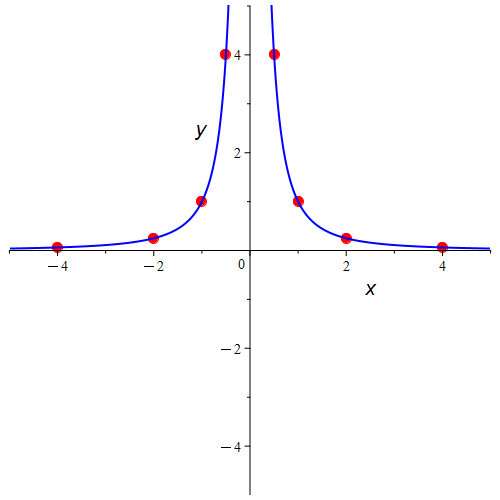
پس نتیجه در مورد حد این تابع زمانی که $x$ به صفر میل میکند این است که مقدار تابع به مثبت بینهایت میل خواهدکرد، یعنی $\lim_{x\to 0}\frac{1}{x^2}=+\infty$.
اکنون به عنوان جایزه برای دوستانی که به نرمافزار و برنامهنویسی علاقهدارند، نمودارهای بالا با نرمافزار میپل Maple و با دستورهای زیر کشیده شدهاند.
y := 1/x:
xlist := [ -4, -2, -1, -1/2, -1/4, 1/4, 1/2, 1, 2, 4 ]:
points := [ seq( [ a, eval( y, x = a ) ], a in xlist ) ]:
p1 := plots:-pointplot( points, symbol = solidcircle, symbolsize = 15, color = red ):
p2 := plot( y, x = -5 .. 5, thickness = 2, color = blue ):
plots:-display( p1, p2, view = [ -5 .. 5, -5 .. 5 ], labels = [ 'x', 'y' ], labelfont = [ "Arial", 16 ] );
y := 1/(x^2):
xlist := [ -4, -2, -1, -1/2, -1/4, 1/4, 1/2, 1, 2, 4 ]:
points := [ seq( [ a, eval( y, x = a ) ], a in xlist ) ]:
p1 := plots:-pointplot( points, symbol = solidcircle, symbolsize = 15, color = red ):
p2 := plot( y, x = -5 .. 5, thickness = 2, color = blue ):
plots:-display( p1, p2, view = [ -5 .. 5, -5 .. 5 ], labels = [ 'x', 'y' ], labelfont = [ "Arial", 16 ] );