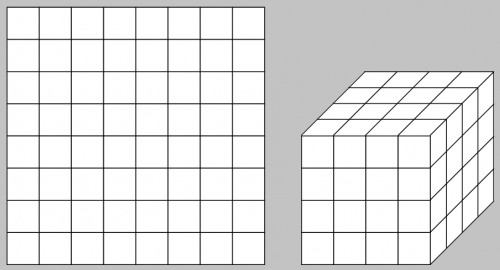
با درود مجدد. فرض کنید $64$ حبه قند کارخانه ای را بشکل مربع
$8^{2}$
چیده ایم.میخواهیم بدانیم اگر بخواهیم آنها را بشکل مکعب بچینیم، در هریک از ابعاد سه گانه آن چند حبه قند خواهیم داشت؟ ابتدا با تعریف رسمی از مرجع معتبر شروع میکنیم و سپس با مثال فوق تطبیق میدهیم.
توانهای کسری: برای تعریف اینکه منظور از توان کسری چیست، نیاز به استفاده از رادیکالها داریم. برای معنا دادن به نماد $ a^{ \frac{1}{n} } $ بطوریکه با قوانین توانها سازگار باشد، کافیست داشته باشیم $(a^{\frac{1}{n}})^{n}=a^{(\frac{1}{n})n}=a^{1}=a$. بنابراین با تعریف ریشه $n$ ام بصورت $a^{\frac{1}{n}}=\sqrt[n]{a}$ ، بطور کلی توانهای کسری را بطریق زیر تعریف میکنیم.
تعریف توانهای کسری: برای تعریف هر توان کسری $\frac{m}{n}$ با کوتاهترین عبارت، که $m$ و $n$ اعداد صحیح بوده و $n>0$ باشد، داریم
$a^{\frac{m}{n}}=(\sqrt[n]{a})^m \Longrightarrow a^{ \frac{m}{n} }=\sqrt[n]{a^{m}}$
با این تعریف، قابل اثبات است که قوانین توانها برای توانهای کسری نیز برقرار است.
مرجع : algebra and trigonometry, James Stewart, Saleem Watson, Lothar Redlin, 4th edition, 2015, Cengage learning, P:27
بررسی تطبیقی با مثال فوق: برای معنا دادن به $ 8^{ \frac{1}{3} } $ بطوریکه با قوانین توانها سازگار باشد، کافیست داشته باشیم
$(8^{ \frac{1}{3} })^{3}=8^{( \frac{1}{3})3 }=8^{1}$
. بنابراین با تعریف ریشه سوم بصورت $8^{ \frac{1}{3} }= \sqrt[3]{8} $ ، توان کسری برای $8$ را بشکل زیر تعریف میکنیم.
تعریف توان کسری برای 8: برای تعریف توان کسری $ \frac{2}{3} $ برای $8$، داریم:
$8^{\frac{1}{3} }×8^{\frac{1}{3}}=8^{\frac{2}{3}}=(\sqrt[3]{ 8})^2 \Longrightarrow 8^{ \frac{2}{3} }=\sqrt[3]{8^{2}}=4$
یعنی عدد تبدیل شونده (در اینجا $8$) به هر شکل ممکن با صورت کسر، زیر رادیکال می آید و مخرج کسر بصورت فرجه ظاهر میشود. بعبارت دیگر عدد مربعی $8^{2}$ را به عدد مکعبی $4^{3}$ تبدیل می کنیم. توجه داشته باشید که تعاریف و خواص مرتبط با اصول موضوعه، اثبات پذیر نیستند بلکه باید با روشهای مبتکرانه آنها را آموخت. موفق باشید.