تابع $|x|$ را با اسپلاین طبیعی بر روی بازهٔ $[-1,1]$ طوری تقریب بزنید که در چهار نقطهٔ $-1$ و $-0.5$ و $0$ و $1$ برابر با مقدار تابع باشد.

Question

تابعِ $f(x)=|x|$ را بر روی بازهٔ $[-1,1]$ در نظر بگیرید. این تابع را با اسپلاین طبیعی تقریب به گونه‌ای تقریب بزنید که اگر این اسپلاین را با $s$ نمایش دهیم، داشته‌باشیم $f(1)=s(1)$، $f(-1)=s(-1)$، $f(-0.5)=s(-0.5)$ و $f(0)=s(0)$.

Answer 1

همیشه یک تلاشی هم از خودتان ارائه کنید. یک جواب بسیط می‌نویسم تا یک نوع آموزش برای دیگران هم باشد. در ابتدا تعریف زیر را مرور می‌کنیم.

تعریف (درون‌یابی اسپلاین مکعبی): به ازای $n+1$ زوج مرتب داده شد‌هٔ
$(x_{n},y_{n}), \dots ,(x_{0},y_{0})$ یک درون‌یابی اسپلاین مکعبی $S$ یک تابع هموار تکه‌ای می‌باشد که در شرایط ذیل صدق نماید:

1. $S(x)$ یک چندجمله‌ای در بازه‌ی $[x_{j},x_{j+1}]$ است که با $S_{j}(x)$ به ازای $j=0,\cdots ,n-1$ نمایش داده می‌شود،
2. به ازای هر $j=0,\cdots ,n-1$ داشته باشیم $S_{j}(x)=y_{j}$ و $S_{j+1}(x)=y_{j+1}$،
3. به ازای هر $j=0,\cdots ,n-2$ داشته باشیم $S_{j+1}(x_j)=S_j(x_{j+1})$،
4. به ازای هر $j=0,\cdots ,n-2$ داشته باشیم $S_{j+1}'(x_j)=S_{j}'(x_{j+1})$،
5. به ازای هر $j=0,\cdots ,n-2$ داشته باشیم $S_{j+1}''(x_{j})=S_{j}''(x_{j+1})$.

حال بیایید تعداد مجهولات و شرایط در تعریف را بشماریم. هر بازه‌ی $[x_{j},x_{j+1}]$ به ازای $j=0,\cdots ,n$، یک چندجمله‌ای از درجه‌ی $3$ دارد. بنابراین $4n$ ضریب داریم. از طرفی هم شرط دوم $n+1$ شرط و شروط سوم تا پنجم $3(n-1)$ شرط، در اختیار ما می‌گذارد. لذا $4n-2$ شرط، برای $4n$ مجهول داریم. بسته به اینکه دو شرط باقیمانده را چگونه انتخاب کنیم، می‌توانیم درون‌یابی اسپلاین مکعبی مختلفی را تعریف کنیم.

تعریف (درون‌یابی اسپلاین مکعبی طبیعی): یک درون‌یابی اسپلاین مکعبی می‌باشد که $$S''(x_{0})=S''(x_{n})=0.$$

حال بیایید به حل مسئله بپردازیم. چون سه بازه‌ی $[-1,-\frac{1}{2}]$، $[-\frac{1}{2},0]$، $[0,1]$ داریم. لذا این اسپلاین شامل سه چندجمله‌ای می‌باشد. پس $$S_{0}(x)=a_{0}+b_{0}(x+1)+c_{0}(x+1)^{2}+d_{0}(x+1)^{3}$$ برای بازه‌ی $[-1,-\frac{1}{2}]$، $$S_{1}(x)=a_{1}+b_{1}(x+1)+c_{1}(x+1)^{2}+d_{1}(x+1)^{3}$$ برای بازه‌ی $[-\frac{1}{2},0]$ و $$S_{1}(x)=a_{1}+b_{1}(x+1)+c_{1}(x+1)^{2}+d_{1}(x)^{3}$$ برای بازه‌ی $[0,1]$. به نوع انتخاب چندجمله‌ای‌ها برای راحتی کار دقت کنید. حال از شروط دوم و سوم داریم که $$S_{0}(-1)=1,\; S_{0}(-\frac{1}{2})=\frac{1}{2}=S_{1}(-\frac{1}{2}), \; S_{1}(0)=0=S_{2}(0),\; S_{2}(-1)=1,$$ پس

• $a_{0}=1$
• $a_{0}+b_{0}(\frac{1}{2})+c_{0}(\frac{1}{2})^{2}+d_{0}(\frac{1}{2})^{3}=\frac{1}{2}$
• $a_{1}=\frac{1}{2}$
• $a_{1}+b_{1}(\frac{1}{2})+c_{1}(\frac{1}{2})^{2}+d_{1}(\frac{1}{2})^{3}=0$
• $a_{2}=0$
• $a_{2}+b_{2}+c_{2}+d_{2}=1$.

حال از شرط چهارم می‌بینیم که $S_{0}'(-\frac{1}{2})=S_{1}'(-\frac{1}{2})$ و $S_{1}'(0)=S_{2}'(0)$. از اینجا داریم

• $b_{0}+2c_{0}(\frac{1}{2})+3d_{0}(\frac{1}{4})=b_{1}$
• $b_{1}+2c_{1}(\frac{1}{2})+3d_{1}(\frac{1}{4})=b_{2}$.

به همین ترتیب از شرط پنجم داریم که

• $2c_{0}+3d_{0}(-\frac{1}{2})=c_{1}$
• $2c_{1}+6d_{1}(\frac{1}{2})=c_{2}$.

در نهایت از شرط درون‌یابی اسپلاین مکعبی طبیعی می‌بینیم که

$$S_{0}''(-1)=S_{2}''(1)=0$$

این یعنی $c_{0}=0$ و $c_{2}+3d_{2}=0$.

اگر همه شروط را در کنار هم بگذاریم، به یک دستگاه معادلات خطی با $12$مجهول می‌رسیم. این ماتریس را می‌توان با هر نرم‌افزار ریاضی (مثلا میپل، متلب، متمتیکا و غیره) حل کرد. در نهایت جواب آخر برابر می‌شود با $$S(x) =\begin{cases} S_{0}(x) & ;\;x\in[-1,-\frac{1}{2}],\\ \\ S_{1}(x) & ;\;x\in[-\frac{1}{2},0],\\ \\ S_{2}(x) & ;\;x\in[0,1]. \end{cases} $$ که در آن $S_{0}(x)=1+(-1.1176)(x+1)+(0.4706)(x+1)^3$، $S_{1}(x)=0.5+(-0.7647)(x+(0.5))+(0.7059)(x+(0.5))^2+(-2.3529)(x+0.5)^3$ و $S_{2}(x)=(-1.8235)(x)+(4.2353)(x)^2+(-1.4118)(x)^3$.

در شکل زیر می‌توانید اسپلاین مورد نظر را ببینید.

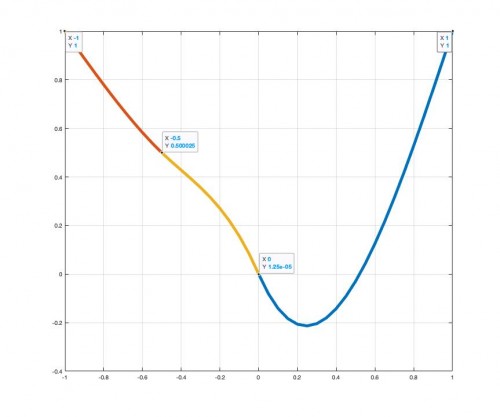
نکته: می‌توان ثابت کرد که در حالت کلی دستگاه معادلات خطی برای محاسبه‌ی ضرایب حاصل از درون‌یابی اسپلاین مکعبی طبیعی همیشه یک جواب منحصربفرد دارد. همچنین می‌توان برنامه‌نویسی حالت کلی‌تری برای درون‌یابی اسپلاین مکعبی طبیعی را انجام داد.