- وسطهای چهار ضلعی مقعر ABCD یک متوازی الاضلاع می باشد. فرض می کنیم قطرها ی چهارضلعی همدیگر را در نقطه G با زاویه بتا $ \beta $ قطع کنند مطابق شکل زیر
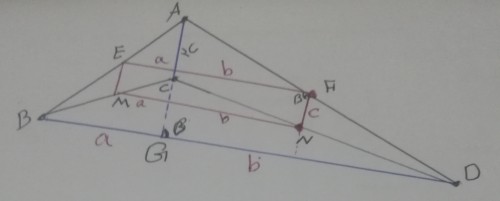
فرض کنید
$$AC=2c,BG=2a,GD=2b,CG=h$$
- مساحت متوازی الاضلاع $EFNM$ برابر است با
$$ S_{EFNM} =(a+b) csin \beta $$
- از طرف داریم
$$S_{ACD} =S_{AGD} - S_{CGD} $$
$$\quad= \frac{1}{2} (2c+h)(2b)sin\beta-
\frac{1}{2} (h)(2b)sin\beta$$
$$S_{ACD}=2bcsin\beta$$
به طور متشابه داریم
$$S_{ACB}=2acsin\beta$$
با یک مقایسه به نتیجه مورد نظر خواهیم رسید