دایره ای داخل یک مستطیل مماس بر سه ضلعش رسم می کنیم. سپس از یک گوشهٔ مستطیل یک مماس بر دایره می کشیم. طول مماس را می خواهیم.

Question

در مستطیل $ABCD$ می‌دانیم $AB=3$ و $BC=2$ است. دایره‌ای به اضلاع $AB,BC,CD$ مماس است. از نقطه $D$ مماسی غیر از $CD$ بر دایره رسم می‌کنیم تا $AB$ را در $P$ قطع کند. طول DP چند است؟

Answer 1

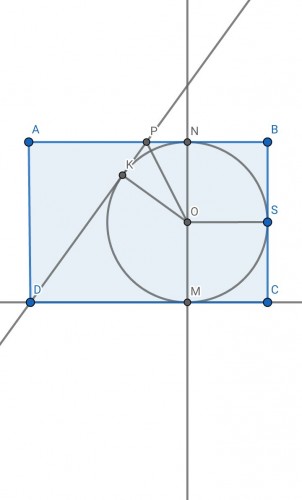
دایره در نقطه $M$ بر ضلع CD مماس است و در نقطه $S$ بر ضلع $BC$ مماس و در نقطه N بر AB و در نقطه k بر $DP$ مماس است.

اگر از مرکز دایره $o$ به نقاط فوق وصل کنیم معلوم می شود که شعاع دایره برابر با یک است. حال داریم:

$ok=oN$

$op=op$

$ \angle N= \angle K=90$

از اینها نتیجه می شود که $pn=pk=y$. حال با توجه به مثلث قائم الزاویه $ADP$ داریم:

$2^2+(2-y)^2=(2+y)^2 \Longrightarrow y= \frac{1}{2} $

پس پاسخ می شود:

$2+ \frac{1}{2}= \frac{5}{2}$

Comments

Elyas1@ پیشنهاد می کنم به کمک نرم افزارهای رسم برای پاسختون شکل ارائه دهید.

---

@good4us چشم. با نرم‌افزارgeogebra سعی میکنم.