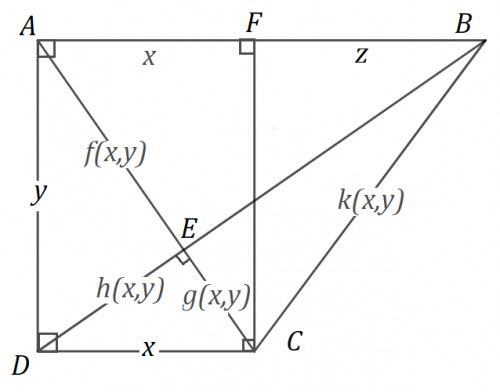
Щ…ЩӮШ§ШҜЫҢШұ AE ЩҲ EC ЩҒЩӮШ· ШЁШұ Ш§ШіШ§Ші x ЩҲ y ЩӮШ§ШЁЩ„ Щ…ШӯШ§ШіШЁЩҮ ЩҮШіШӘЩҶШҜ. Ш§ЫҢЩҶ ЪҜШІШ§ШұЩҮ ШЁШ§ Ш§ШіШӘЩҒШ§ШҜЩҮ Ш§ШІ Щ…Ш№Ш§ШҜЩ„ЩҮ ШІЫҢШұ Ш«Ш§ШЁШӘ Щ…ЫҢ ШҙЩҲШҜ:
$ \sqrt{y^{2}-DE^{2}}+\sqrt{x^{2}-DE^{2}}=\sqrt{x^{2}+y^{2}} $
ШЁШ§ Щ…ШӯШ§ШіШЁЩҮ DE ШҜШұ ЩҒШұЩ…ЩҲЩ„ Щ…Ш№Ш§ШҜЩ„ЩҮ ШЁШ§Щ„Ш§ AE ЩҲ EC ШЁЩҮ ШөЩҲШұШӘ $ \sqrt{AE^{2}-DE^{2}}=AE $ ЩҲ $ \sqrt{DC^{2}-DE^{2}}=EC $ Щ…ШӯШ§ШіШЁЩҮ Щ…ЫҢ ШҙЩҲЩҶШҜ.
Щ…ЩӮШҜШ§Шұ BE ЩҶЫҢШІ ШЁШ§ Ш§ШіШӘЩҒШ§ШҜЩҮ Ш§ШІ ШӘШҙШ§ШЁЩҮ ШҜЩҲ Щ…Ш«Щ„Ш« DEC ЩҲ AEB Щ…ШӯШ§ШіШЁЩҮ Щ…ЫҢ ШҙЩҲШҜ. ШҜШұ ЩҶШӘЫҢШ¬ЩҮ Щ…ЩӮШҜШ§Шұ BC ЩҶЫҢШІ Щ…ШӯШ§ШіШЁЩҮ Щ…ЫҢ ШҙЩҲШҜ. ($ BC=\sqrt{EC^{2}+EB^{2}} $) ШҜШұ ЩҶШӘЫҢШ¬ЩҮ Щ…ЩӮШҜШ§Шұ FB ЩҶЫҢШІ Щ…ШӯШ§ШіШЁЩҮ Щ…ЫҢ ШҙЩҲШҜ. ($ FB=\sqrt{BC^{2}-y^{2}} $) Ш§ЫҢЩҶ ШЁШҜЫҢЩҶ Щ…Ш№ЩҶЫҢ Ш§ШіШӘ Ъ©ЩҮ FB ЩҒЩӮШ· ШЁШұ Ш§ШіШ§Ші x ЩҲ y Щ…ШӯШ§ШіШЁЩҮ ШҙШҜЩҮ Ш§ШіШӘ.
Щ…ШіШҰЩ„ЩҮ Ш®ЩҲШ§ШіШӘЩҮ Ш§ШіШӘ Ш«Ш§ШЁШӘ Ъ©ЩҶЫҢЩ… $ y^{2}=x(x+z) \Rightarrow z=\frac{y^{2}-x^{2}}{x} $. Ъ©Ш§ЩҒЫҢШіШӘ Щ…ЩӮШҜШ§ШұЫҢ Ъ©ЩҮ Щ…ШӯШ§ШіШЁЩҮ Ъ©ШұШҜЫҢЩ… ШұШ§ ШЁШ§ Ш№ШЁШ§ШұШӘ $ \frac{y^{2}-x^{2}}{x} $ Щ…ЩӮШ§ЫҢШіЩҮ Ъ©ЩҶЫҢЩ….