با سلام
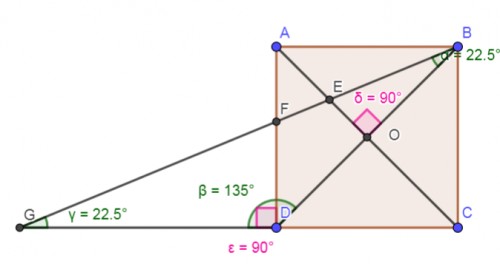
می دانیم که در مربع ، قطرها با هم برابرند ، بر هم عمودند ، یکدیگر را نصف می کنند و نیمساز زوایا هستند.
$ \triangle DBG: \alpha =22.5 \beta =135 \Rightarrow \gamma =22.5 \Rightarrow DG=DB=2OB $
همچنین مثلث های زیر ( بنا به حالت دو زاویه برابر ) با هم متشابه هستند.
$ \triangle OEB \sim \triangle DFG \Rightarrow \frac{OE}{DF} = \frac{OB}{DG} \Rightarrow \frac{14}{DF} = \frac{OB}{2OB} \Rightarrow DF=2 \times 14=28 $