دو سر متقابل یک کاغذ مستطیلی شکل به ابعاد ۶ در ۸ را روی هم قرار داده و کاغذ را روی هم فشرده طول خط تا ایجاد شده را بیابید.

Question

دو سر متقابل( دو راس روی یک قطر) یک کاغذ مستطیلی شکل به ابعاد ۶ در ۸ را روی هم قرار داده و کاغذ را روی هم فشرده ،طول خط تا ایجاد شده را بیابید

Answer 1

به نام خدا.

پس از اینکه کاغذ را تا کردیم پاره خط $EF$ پدید می آید. حال مثلث $EFB$ را ایجاد کنید. یک بار دیگر کاغذ را تا کنید. واضح است که مثلث $CEF$ قرینه یافته مثلث$EFB$ نسبت به ضلع $EF$ است.

توجه کنید در شکل:

$CE=BE=CF=BF$

حال داریم:

$AE+BE=8$

$36+AE^2=CE^2=BE^2$

پس از حل معادله فوق به نتیجه زیر می رسیم:

$AE= \frac{7}{4} $

$BE= \frac{25}{4} $

توجه کنید که:

$sin \angle ACE=cos \angle ECF= \frac{7}{25}$

مثلث $ECF$ متساوی الساقین است و به کمک قضیه کسینوس ها می توان $EF$ را بدست آورد:

$EF= \frac{15}{2}$

Comments

شکل عالی رسم کردید
در خط دوم D  را به F اصلاح کنید و در آخر اثبات به جای قضیه کسینوس ها می توانستید با رابطه فیثاغورس  راحتر کنید.

---

کسینوس زاویه ECF چگونه بدست آمده است؟

---

@seiedirani زاویه $ACE$ متمم $ECF$ متمم اند. یا
بنابر دو خط موازی و یک خط مورب $ECF=CEA$

Answer 2

با سلام

با دیدن پاسخ آقای @Elyas1 و اینکه در ابتدا ذکر کردند چهار ضلعی CEBF لوزی است این راه به ذهنم رسید.

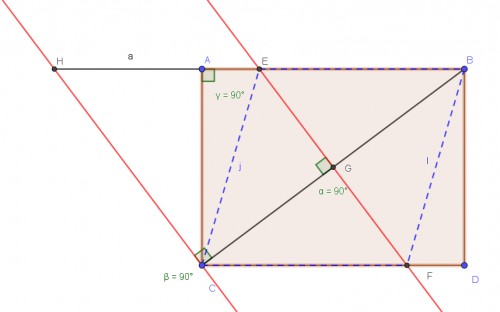
می دانیم که در لوزی قطرها بر هم عمودند. از نقطه C خطی موازی EF رسم می کنیم تا امتداد AB را در نقطه H قطع کند.

$ \bigtriangleup CHB : CA \bot BH , \beta =90 \Longrightarrow CA^{2}=AH \times AB \Longrightarrow 6^{2}=a \times 8 \Longrightarrow a= \frac{9}{2} $ $ \bigtriangleup ACH : HC^{2} = (\frac{9}{2}) ^{2}+ 6^{2} \Longrightarrow HC= \frac{15}{2 } \Longrightarrow EF= \frac{15}{2} $