گسترده یک چهار وجهی مثلث $ABC$ می باشد. اضلاع مثلث $ABC$ کدامیک از موارد زیر می باشد ؟چرا؟

Question

گسترده یک چهار وجهی ، مثلث $ABC$ می باشد. اضلاع مثلث $ABC$ کدامیک از موارد زیر می تواند باشد ؟چرا؟

1. طول اضلاع 8،6و10
2. طول اضلاع 8،5و10
3. طول اضلاع 7،6و10
4. طول اضلاع 8،6و9

Comments

@amir7788  با توجه به قائم الزاویه بودن مثلث گزینه 1 فکر میکنم در صورتی که وسط های اضلاع آن را به هم وصل کنیم چهار مثلث قائم الزاویه همنهشت پدید می آید که میتواند گزینه مطلوب باشد

---

گزینه 1 اشتباه است چون چهار وجهی ایجاد نمی شود

Answer 1

جهت ایجاد یک ذهنیت کلی و ادامه توضیحات تصویر زیر را در نظر بگیرید:

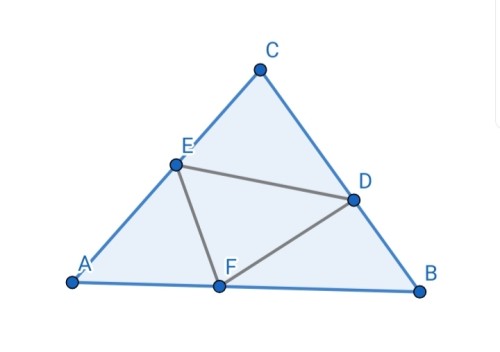
فرض میکنیم $ABC$ گسترده یک چهار وجهی است. در این صورت پس از تا کردن صفحه یا همان کاغذ حول $DE$، $EF$ و $DF$ نقاط $A$، $B$ و $C$ باید بر هم منطبق شوند. برای مثال اگر قرار باشد $A$ و $B$ منطبق شوند، به این معنیست که $AF$ و$ BF$ باید روی هم قرار بگیرند بنابراین $AF=BF$ و به همین ترتیب نتیجه میگیریم نقاط $D$ و $E$ و $F$ وسط اضلاع هستند و به کمک تالس ثابت میشود خطوط تا موازی اضلاع هستند (از این مورد بعدا استفاده خواهیم کرد)

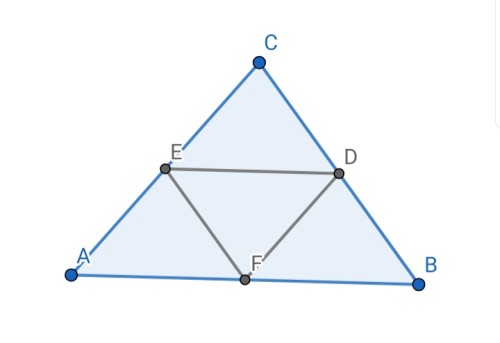
برای آنکه صفحه را حول $FE$ تا کنیم باید $A$ را نسبت به $FE$ دوران دهیم بنابراین اگر از بالا به صفحه نگاه کنیم $A$ همواره روی خط $AG$ است ($G $ پای عمود وارد بر $FE$ توسط $A$ است) و از آنجا که $FE$ با $BC$ موازی است، خط $AG$ همان ارتفاع مثلث است بنابراین در صورت تشکیل چهاروجهی با نگاه از بالا راس چهار وجهی نقطه $J$ یعنی نقطه همرسی ارتفاع های مثلث $ABC$ خواهد بود:

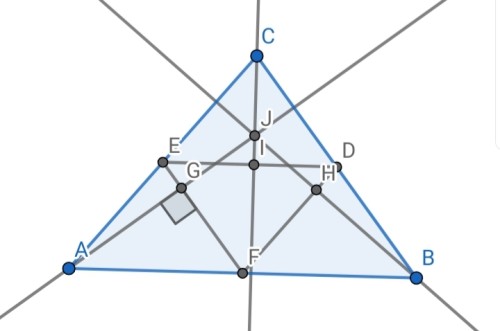
اگر $J$ هر نقطه ای غیر از داخل مثلث باشد چهاروجهی تشکیل نمیشود زیرا نقاط با دوران حول خط تایشان نمیتوانند به آن نقطه برسند. برای درک بهتر این موضوع به تصویر زیر توجه کنید که در آن $J$ خارج از مثلث است:

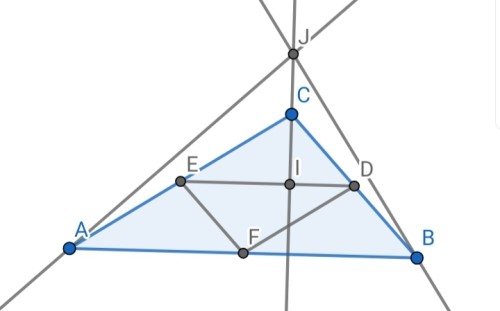
فاصله $C$ تا $DE$ همواره برابر $CI$ است. از طرفی قرار است $C$ با دوران حول $DE$ به $J$ برسد اما حتی در حالتی که $J$ روی صفحه شامل $ABC$ باشد هم فاصله $J$ تا $I$ بیشتر از $CI$ است (و در حالتی که روی صفحه مذکور نباشد به علت افزایش ارتفاع این فاصله بیشتر هم خواهد شد) بنابراین $J$ در نگاه دو بعدی باید داخل مثلث باشد و این تنها زمانی رخ میدهد که مثلث حاده باشد (توجه کنید اگر مثلث قائم الزاویه باشد مرکز ارتفاعی روی راس قائمه خواهد بود و حاصل حجمی سه بعدی نیست بلکه مستطیلی در صفحه تشکیل میدهد یعنی یکی از خطوط تا بدون استفاده مانده و دوتای دیگر دورانی $180$ درجه ای دارند)

حال وقت آن رسیده که نگاهی به گزینه ها بیندازیم اما پیش از نتیجه گیری هنوز باید لم دیگری را اثبات کنیم ...

لم :

در مثلثی به اضلاع $a$، $b$ و $c$ اگر داشته باشیم $a^2+b^2\le c^2$ مثلث حاده نیست.

اثبات :

طبق فرض مسئله داریم

$a^2+b^2\le c^2$

همچنین با توجه به قانون کسینوس ها میدانیم

$c^2=a^2+b^2-2ab\cdot cosC$

با جایگذاری $c^2$ در نامساوی داریم

$a^2+b^2\le a^2+b^2-2ab\cdot cosC $

$\Rightarrow 2ab\cdot cosC \le 0 $

$\Rightarrow cosC \le 0 $

$\Rightarrow 90° \le C \lt 180°$

بنابراین مثلث یا قائمه و یا منفرجه است یعنی حاده نیست.

در گزینه ها داریم

1. $6^2+8^2\not\gt10^2$
2. $5^2+8^2\not\gt10^2$
3. $6^2+7^2\not\gt10^2$
4. $6^2+8^2\gt9^2$

پس پاسخ مطلوب گزینه 4 است.