در شکل آمده در متن پرسش که تعدادی چهارخانه در کنار هم هستند، به چند روش از پائین و چپ ترین نقطه می توان به بالا و راست ترین نقطه رفت؟

Question

در شکل زیر اگر روی خط‌ها تنها به سمت راست یا بالا بتوان حرکت کرد، به چند طریق می‌توانیم از نقطهٔ $A$ به نقطهٔ $B$ رفت؟

لطفاً روش حل اینگونه پرسش را توضیح دهید.

Comments

از نقطه آ تا نقطه ب سی راه وجود داردبا شرط این که فقط به راست یا بالا حرکت کنیم.

Answer 1

به نام خدا.

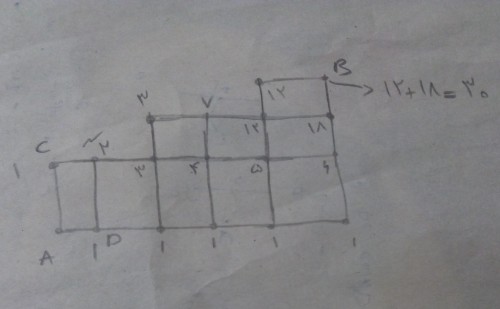
در شکل زیر هر عدد نشان دهنده تعداد راه های رسیدن به رأس کنار آن را بیان می کند. تعداد راه های رسیدن به رأس های پایین همگی برابر با $1$ است زیرا تنها می توان به سمت راست رفت تا به آنها رسید.

در شکل زیر تعداد راه های رسیدن به هر رأس مانند $N$ برابر جمع تعداد راه های رسیدن به $C,D$ است. همین روند را ادامه دهید تا به جواب برسید.

پس از دیدن حل این سوال پیشنهاد می کنم سعی کنید مسئله شماره $14$ المپیاد ریاضی دانش آموزی مرحله اول 1384 را نیز حل کنید.

Answer 2

یک راه برای رسیدن از A به B این است :

$URRURRUR$

در اینجا منظور از R حرکت به راست است و منظور از U حرکت به بالا. حال تعداد جایگشت های این حروف را حساب کنید. میشود 8 فاکتوریل ... حال تقسیم بر جایگشت های تکراری کنیم. خلاصه به صورت زیر است :

$\frac{8!}{3! \cdot 5!} = 56$

Comments

اگر یک مستطیل $5$ در $3$ بود، آنگاه پاسخ شما درست خواهد بود ولی شکل مستطیل کامل نیست.

---

ضمن تشکر از پاسخ شما میخواستم به اطلاعتون برسونم که طبق پاسخنامه منبع جواب میشود ۳۰  فکر میکنم در جایی از جوابتان مشکلی وجود دارد
( منبع : کتاب نشر الگو ریاضی دهم تست ۴ درسنامه فصل ۶)

---

@M.hjz می‌توانید منبع پرسش را در قسمت مرجع پرسش بیفزائید. @sMs دیدگاه آقای @Elyas1 درست است.