Question

به ازای کدام مقادیر x،حاصل |x+1|+|x_1/2| به x بستگی ندارد؟ ۱)ایکس ها کوچکتر مساوی ۱- ۲)ایکس های بزرگتر مساوی ۱/۲ ۳)ایکس های بزرگتر مساوی۱/۲- و کوچکتر مساوی ۱ ۴)ایکس های بزرگتر مساوی ۱- و کوچکتر مساوی ۱/۲ جواب گزینه ۴ میشود اما سوال من اینه که ۱- در سه گزینه مشترکه پس چرا گزینه ها دیگ درست نیستند و در خود گزینه چهار ۱/۲ باعث میشه عبارت مثبت شود و به xوابسته شود اما در صورتی که در جواب گفته هر عددی بین بازه گفته شده باعث میشود xها حذف شده و به x بستگی نداشته باشد.

Comments

@sammmm لطفا تایپ ریاضی را راهنمای سایت بیاموزید

---

Sammmm@ این تابع که به گلدانی معروف است
در بازهٔ بین ریشه های درون قدر مطلق ها ثابت است به تعیین علامت درون آنها و خروج از قدر مطلق دقت کنید

Answer 1

اگر عبارت $|x+1|$ رو تعیین علامت کنید می بنید که زمانیکه $x>-1$ است عبارت همواره مثبت است و می تواند از قدرمطلق خارج شود.

با تعیین علامت علامت عبارت $|x- \frac{1}{2} |$ نیز خواهید دید که تابع برای $x$ های کوچکتر از منفی نیم همواره منفی است. پس در بازه بین -1 و 0.5 $|x+1|$ همواره مثبت است و می تواند از داخل قدرمطلق به شکل $x+1$ خارج شود و همچنین عبارت $|x- \frac{1}{2} |$ همواره منفی است و قرنیه آن می تواند از قدر مطلق خارج شود.

لذا در این بازه خواهیم داشت: $|x+1|+|x- \frac{1}{2} | = x+1+ \frac{1}{2}-x = 1.5 $

همانطور که می بیند متغیر x حذف شد و در این بازه متغیر x تاثیری در جواب تابع ندارد.

در مورد سوالات شما: اینکه -1 در هر سه گزینه وجود دارد طبیعی است. وقتی جواب قرار است بازه باشد ممکن است گزینه های غلط نیز بخشی از بازه صحیح را شامل شوند. اما گزینه ای صحیح است که تمام بازه صحیح را مشخص کند و نه یک نقطه از آن و یا حتی بخشی از بازه صحیح را.

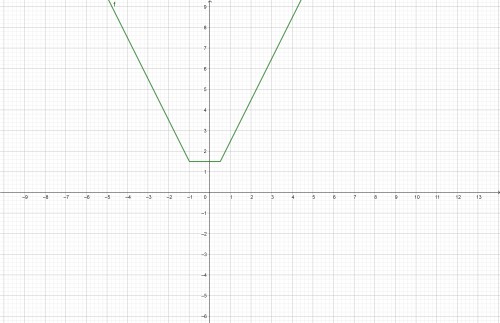
اگر شکل زیر رو مشاهده کنید خیلی بهتر متوجه ثابت نمودار تابع در محدوده جواب خواهید شد.