Ш§ШІ ЩҮШұ 20 ЩҶЩҒШұ 9 ЩҶЩҒШұ ШҜШ®ШӘШұ ЩҲ 11 ЩҶЩҒШұ ЩҫШіШұ ЩҮШіШӘЩҶШҜЩҫШі $ \frac{9}{20} $ Ш§ШІ $5400$ ЩҶЩҒШұ ШҜШ®ШӘШұ ЩҲ $ \frac{11}{20} $ Ш§ШІ $5400$ ЩҶЩҒШұ ЩҫШіШұ ЩҮШіШӘЩҶШҜ . ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ ШӘШ№ШҜШ§ШҜ ШҜШ®ШӘШұШ§ЩҶ ЩҲ ЩҫШіШұШ§ЩҶ ШЁЩҮ ШӘШұШӘЫҢШЁ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ :
$$ \frac{9}{20} \times 5400=2430$$
$$\frac{11}{20} \times 5400=2970$$
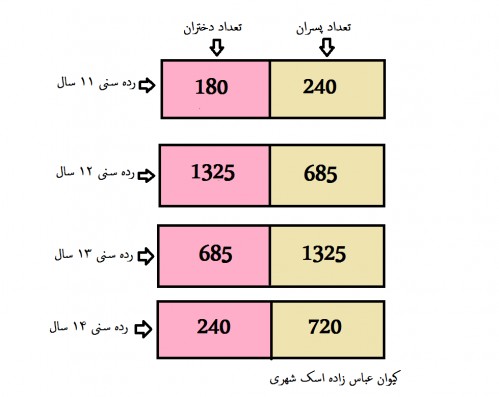
ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Щ…ЩҒШұЩҲШ¶Ш§ШӘ Щ…ШіШҰЩ„ЩҮ Щ…ЫҢ ШӘЩҲШ§ЩҶ ЩҶЩ…ЩҲШҜШ§ШұЩҮШ§ЫҢ ШІЫҢШұ ШұШ§ ШұШіЩ… Ъ©ШұШҜ : ( ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ Ш·ШЁЩӮ ЩҒШұШ¶ Щ…ШіШҰЩ„ЩҮ ШӘШ№ШҜШ§ШҜ ЩҫШіШұШ§ЩҶ 14 ШіШ§Щ„ Ш§ШІ ШӘШ№ШҜШ§ШҜ ЩҫШіШұШ§ЩҶ 12 ШіШ§Щ„ ЫҢШ§ ШӘШ№ШҜШ§ШҜ ШҜШ®ШӘШұШ§ЩҶ 13 ШіШ§Щ„ 35 ЩҶЩҒШұ ШЁЫҢШҙШӘШұ Ш§ШіШӘ ЩҫШі ШӘШ№ШҜШ§ШҜ ЩҫШіШұШ§ЩҶ 12 ШіШ§Щ„ ШЁШ§ ШӘШ№ШҜШ§ШҜ ШҜШ®ШӘШұШ§ЩҶ 13 ШіШ§Щ„ ШЁШұШ§ШЁШұ Ш§ШіШӘ )
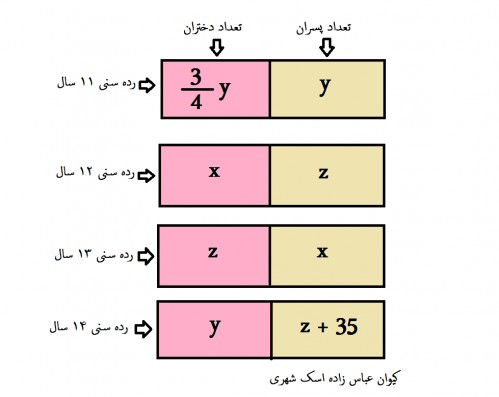
ШӘШ№ШҜШ§ШҜ ШҜШ®ШӘШұШ§ЩҶ $2430$ ЩҶЩҒШұ Ш§ШіШӘ ЩҫШі ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ ЩҶЩ…ЩҲШҜШ§ШұЩҮШ§ЫҢ ШЁШ§Щ„Ш§ ШҜШ§ШұЫҢЩ… :
$$ \frac{3}{4} y+x+z+y=2430 \ \ \ \ast $$
ШӘШ№ШҜШ§ШҜ ЩҫШіШұШ§ЩҶ $2970$ ЩҶЩҒШұ Ш§ШіШӘ ЩҫШі ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ ЩҶЩ…ЩҲШҜШ§ШұЩҮШ§ЫҢ ШЁШ§Щ„Ш§ ШҜШ§ШұЫҢЩ… :
$$y+z+x+z+35=2970$$
Ш§ЪҜШұ Щ…Ш№Ш§ШҜЩ„ЩҮ ШҜЩҲЩ… ШұШ§ Щ…ЩҶЩҮШ§ЫҢ Щ…Ш№Ш§ШҜЩ„ЩҮ Ш§ЩҲЩ„ Ъ©ЩҶЫҢЩ… Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ :
$$z- \frac{3}{4} y+35=540 \ \ \ \clubsuit $$
Ш§ШІ Ш·ШұЩҒЫҢ ЩҶШіШЁШӘ ШӘШ№ШҜШ§ШҜ ШҜШ®ШӘШұШ§ЩҶ 14 ШіШ§Щ„ ШЁЩҮ ЩҫШіШұШ§ЩҶ 14 ШіШ§Щ„ 1 ШЁЩҮ 3 Ш§ШіШӘ ЩҫШі :
$$ \frac{y}{z+35} = \frac{1}{3} $$
Ъ©ЩҮ ШЁШ№ШҜ Ш§ШІ Ш·ШұЩҒЫҢЩҶ ЩҲШіШ·ЫҢЩҶ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ :
$$3y-z=35 \ \ \ \spadesuit $$
ЩҫШі ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Щ…Ш№Ш§ШҜЩ„Ш§ШӘ $ \clubsuit $ ЩҲ $ \spadesuit $ ШҜШіШӘЪҜШ§ЩҮ 2 Щ…Ш№Ш§ШҜЩ„ЩҮ 2 Щ…Ш¬ЩҮЩҲЩ„ ШІЫҢШұ ШұШ§ ШҜШ§ШұЫҢЩ… :
$$z- \frac{3}{4} y+35=540$$
$$3y-z=35$$
ШЁШ№ШҜ Ш§ШІ ШӯЩ„ ШҜШіШӘЪҜШ§ЩҮ Щ…ЩӮШ§ШҜЫҢШұ $y$ ЩҲ $z$ Ш№ШЁШ§ШұШӘЩҶШҜ Ш§ШІ :
$$y=240 \ \ \ \ \ z=685$$
ШЁШ№ШҜ Ш§ШІ Ш¬Ш§ЪҜШ°Ш§ШұЫҢ ШҜШұ Щ…Ш№Ш§ШҜЩ„ЩҮ $ \ast $ Щ…ЩӮШҜШ§Шұ $x$ ШЁШұШ§ШЁШұ $1325$ Ш§ШіШӘ .
ШӯШ§Щ„ ШЁЩҮ ШұШ§ШӯШӘЫҢ Щ…ЫҢ ШӘЩҲШ§ЩҶ ШӘШ№ШҜШ§ШҜ ЩҫШіШұШ§ЩҶ ЩҲ ШҜШ®ШӘШұШ§ЩҶ ЩҮШұ ШұШҜЩҮ ШіЩҶЫҢ ШұШ§ ШЁШҜШіШӘ ШўЩҲШұШҜ .