\begin{cases}x+y+z+t=6\\ \sqrt{1-x²}+ \sqrt{4-y²}+\sqrt{9-z²}+\sqrt{16-t²}=8\end{cases}

Question

اگر $ \ x , y , z , t \in R $ ، و $ x < y < z < t $ با توجه به اطلاعات زیر حاصل $xyzt$ را بیابید.

$\begin{cases} x + y + z + t = 6 \\ \sqrt{ 1 - x² } + \sqrt{ 4 - y² }+\sqrt{ 9 - z² } + \sqrt{ 16 - t² } = 8 \end{cases}$

Answer 1

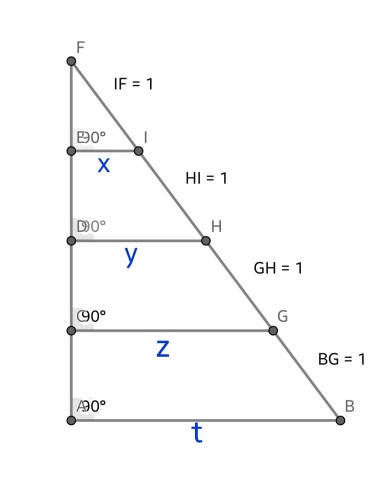
سوال را به شیوه هندسی حل میکنیم. مطابق شکل بالا، مثلث $ABF$ قائم الزاویه است. پاره خط های $AB,CG,DH,EI$ با هم موازی اند.با توجه به شکل اندازه پاره خط های زیر برابر است با: $$EF= \sqrt{1-x²}$$ $$ED= \sqrt{4-y²}- \sqrt{1-x²} $$ $$CD= \sqrt{9-z²}- \sqrt{4-y²} $$ $$CD= \sqrt{16-t²}- \sqrt{9-z²} $$ اطلاعات بالا با صورت سوال مطابقت دارد. حال برای حل سوال از قضیه تالس استفاده می کنیم و می توان نتیجه گرفت: $$ \frac{x}{y}= \frac{1}{2} , \frac{x}{z}= \frac{1}{3} , \frac{x}{t}= \frac{1}{4} $$ $$ \Longrightarrow y=2x , z=3x , t=4x$$ $$ \Longrightarrow x+2x+3x+4x=6$$ $$ \Longrightarrow x=\frac{3}{5} $$ $$\Rightarrow xyzt=24 x^{4}= \frac{1944}{625} $$

Comments

@Dana_Sotoudeh
پاسخی که شما دادید با این فرض است که
$x<y<z<t$
می باشد. سوالی که پیش می آید این است که از کجا می دانید که چنین نامساوی هایی برقرار است؟ لذا به نظرم این تنها پاسخ نیست.

---

ببخشید محاسبه  EF, ED,.... چه تاثیری در راه حلتان داره. با حذف کردن آنها چه مشکلی در اثبات په وجود می آید؟ضمنا از کجا متوجه شدید متغیره ها مثبت هستند؟

---

بله با روش شما یکی از دسته جواب ها بدست می آید.
ولی آیا می توان نشان داد دسته جواب دیگری وجود ندارد؟

---

بله درست می فرمائید الان دیدم اون شرط رو در سوال تایپ نکردم ، ممنون از شما

---

کدام شرط تایپ نکردید بعد از 9 ساعت از پیامت هنوز ویرایش صورت نگرفت،

---

سلام مجدد ، متاسفانه خواستم ویرایش کنم ، نمیدونم به چه دلیلی مشکل پیش میومد؛ممنون میشم شما ویرایش کنید چون چند بار با مشکل مواجه شدم. باید شرط $x<y<z<t$ رو می‌نوشتم که تو سوال یادم رفت ذکرش کنم.

---

چندین بار ویرایش کردم حتی توضیحات اضافه دادم که خطای حداقل 100 کاراکتر از بین بره اما موفق نشدم. در هر صورت  با اضافه کردن این شرط هم، جواب اولین دیدگاه ام نمی باشه. از کجا می دانید متغیرها مثبت اند؟ چون مثلث در صورت مثبت بودن می توان رسم کرد.

---

@dana_sotoudehدر حل مسئله مثلث کوچک را در صورتی می توان رسم کرد که از دو موضوع مطمئن باشیم اول اینکه x مثبت باشه دو م اینکه x کوچکتر از 1 باشه. برای همین این راه حل برایم قابل قبول نمی باشه.
به سوال خوب شما امتیاز دادم اما به راه حل ارائه شده امتیاز ندادم.