ШЁЩҮ ЩҶШ§Щ… Ш®ШҜШ§.
.
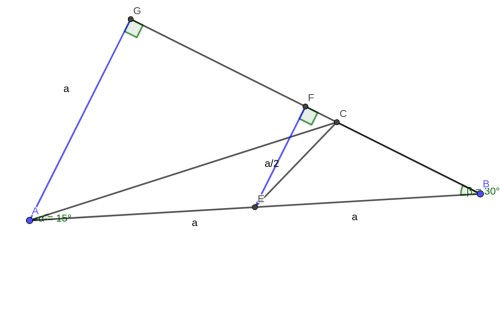
Ш§ШЁШӘШҜШ§ Ш§ШІ $M$ ЩҲ $A$ ШҜЩҲ Ш№Щ…ЩҲШҜ ШЁШұ $BC$ ЩҲШ§ШұШҜ Щ…ЫҢ Ъ©ЩҶЫҢЩ… ЩҲ ЩҶЩӮШ§Ш· ШЁШұ Ш®ЩҲШұШҜ ШўЩҶЩҮШ§ ШұШ§ $F,G$ Щ…ЫҢ ЩҶШ§Щ…ЫҢЩ…. ШӯШ§Щ„ Щ…ЫҢ ШӘЩҲШ§ЩҶ ЩҶЩҲШҙШӘ:(ШЁШұШ§ЫҢ ШұШ§ШӯШӘЫҢ Ъ©Ш§Шұ ЩҒШұШ¶ ШҙШҜЩҮ Ъ©ЩҮ $AM=BM=a$)
$sin(30) =\frac{MF}{a} \Longrightarrow MF= \frac{a}{2} $
$cos30= \frac{BF}{a} \Longrightarrow BF= \frac{ \sqrt{3} a}{2} $
$sin(30)= \frac{AG}{AB}= \frac{AG}{2a} \Longrightarrow AG=a$
$ \angle ACG + \angle ACB=180 \Longrightarrow \angle ACG= 45
\Longrightarrow AG=CG=a$
Щ…ЫҢ ШӘЩҲШ§ЩҶ ШЁШ§ ЩӮШ¶ЫҢЩҮ ШӘШ§Щ„Ші ЩҒЩҮЩ…ЫҢШҜ Ъ©ЩҮ
$BF=FG= \frac{ \sqrt{3} a}{2} $
ШӯШ§Щ„ Щ…ЫҢ Ш®ЩҲШ§ЩҮЫҢЩ… Ъ©ЩҮ Ш§ЩҶШҜШ§ШІЩҮ $CF$ ШұШ§ ШЁЫҢШ§ШЁЫҢЩ…. Щ…ЫҢ ШӘЩҲШ§ЩҶ ЩҶЩҲШҙШӘ:
$CF=CG-FG=a- \frac{ \sqrt{3} a}{2}= \frac{a(2- \sqrt{3}) }{2} \Longrightarrow tan( \angle FMC)= \frac{CF}{FM} = \frac{\frac{a(2- \sqrt{3}) }{2}}{ \frac{a}{2} } =2- \sqrt{3} \Longrightarrow \angle CMF=15 $
ЩҫШі Щ…ЫҢ ШӘЩҲШ§ЩҶ ЩҶЩҲШҙШӘ:
$ \angle CMF+ \angle MCA+ \angle ACG=90 \Longrightarrow \angle ACM=30 \Longrightarrow \angle CMB=30+15=45$