دایره ای را به شعاع یک واحد را در نظر بگیرید، اگر خطی از وسط این دایره رد شود، بدیهی است که مجموعه نقاط روی خط و مجموعه نقاط روی دایره هردو نامتناهی می باشند، این دو مجموعه را مقایسه کنید کدام بزرگ تر است؟
تلاش :
دو دیگاه مطرح می شود
اول :اینکه اگرخط عبوری از وسط دایره را دورتادور محیط دایره بپیچیم، روشن است که طول خط از محیط دایره بزرگ تر است بنا براین مجموعه نقاط روی خط، مجموعه بزرگ تری است.
دوم :اما در مقابل اگر نقطه ای روی دایره را انتخاب کنیم و از ان خطوطی را به دایره وصل کنیم به نحوی که خطوط هم محیط و هم خود خط راقطع کنند، مجموعه نقاط باهم برابر میشوند ولی خود نقطه مورد نظر ما باعث میشود که دایره یک نقطه بیشتر نسبت به خط داشته باشد.( هندسه جبری)
پس ایا این دو مجموعه باهم برابرند؟ چگونه میتوان برای دیدگاه دوم تابعی طرح کرد؟ چگونه از هندسه جبری استفاده میکنید و برای مختصات نقاط تابع مینویسید؟
تصویر سوال را اضافه کردم
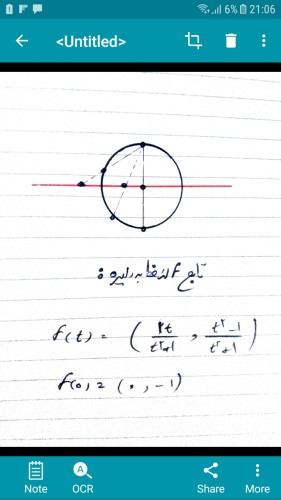
میخواهم بدانم، چگونه با استفاده از این روش ثابت شده مجموعه نقاط روی دایره از خط به اندازه یک نقطه بیشتر است.