چیزی که مطرح کردید، تمرین کتاب نیست! بلکه یک مثال است که خیلی هم روشن و واضح توضیح دادهشدهاست. پس مشکل اصلی شما زبان انگلیسی است. به هر حال من برایتان اینجا پاسخی را مینویسم که پیش از خواندنِ متن کتاب انجام دادم. بعلاوه همیشه مشخصات کتاب را کامل و همانطور که در خود کتاب نوشتهشدهاست بنویسید و از تلگرافی اشاره کردن و تغییر دادن نامها خودداری کنید!
ابتدا گرهٔ $b$ را کمی به سمتِ راست جابجا میکنیم تا شیوهٔ نامگذاریمان در زیر سادهتر شود. توجه کنید که این جابجایی تغییری در شبکه (گراف) ایجاد نمیکند. پس شکلِ زیر را داریم.
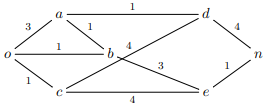
توجه کنید که در شکلِ جدید هیچ یالی به طور دقیقا عمودی نمایش داده نشدهاست پس میتوان از گرهٔ چپ و راست برای یالها صحبت کرد. اکنون به هر یال یک عدد صحیح به این شکل اختصاص دهید که اگر گرهٔ چپِ یالی چپتر از گرهٔ چپِ یالِ دیگری بود، آنگاه یالِ نخست شمارهٔ کوچکتری داشته باشد، در غیر اینصورت، یالی که گرهٔ چپش بالاتر از گرهٔ چپ یال دیگر است را شمارهٔ کوچکتر بدهید. و اگر گرهٔ چپِ هر دو یال یکسان است، آنگاه یالی که گرهٔ راستش چپتر یا بالای گرهٔ راستِ یال دیگر است را شمارهٔ کوچکتر دهید. چون هیچ دو یالِ متمایزی دارای دو گرهٔ یکسان نیستند و یال عمودی نداریم، پس این شمارهگذاری خوشتعریف است با توجه به اینکه از شمارهٔ ۱ شروع میکنیم و یک واحد یک واحد شمارهها را افزایش میدهیم. بنابراین یالِ وصلکنندهٔ گرههای $o$ و $a$ یالِ یکُم است و یا یالِ وصلکنندهٔ گرههای $e$ و $n$ یال دهُم.
متغیرهای صحیحمقدارِ $x_i$ را برای $i=1,\dots,10$ را برای شارِ یالِ $i$اُم تعریف کنید. مقدارِ $x_i$ مثبت است اگر شار به سمت راست باشد و منفی است اگر به سمت چپ باشد. برای کمترنویسی، بردارِ سطریِ $w$ را اینگونه تعریف کنید که درایهٔ $i$اُمش برابر با بیشینهٔ مقدارِ مجازِ شار در یالِ $i$اُم باشد. پس داریم
$$w=(3,1,1,1,1,4,4,3,4,1)$$
هدفِ پرسش، یعنی بیشنه کردنِ نرخِ شار از $o$ به $n$ با شرطهای گذاشتهشده همارز با بهینهسازیِ خطیِ صحیحِ زیر است.
$$
\begin{array}{l}
\begin{array}{ll}
\max & \qquad x_9+x_{10} \\
\text{s.t} & \left\lbrace\begin{array}{ll}
x_1-x_4-x_5 & =0\\
x_2+x_5-x_8 & =0\\
x_3-x_6-x_7 & =0\\
x_4+x_6-x_9 & =0\\
x_7+x_8-x_{10} & =0
\end{array}\right.
\end{array}\\
x_i\in\mathbb{Z},-w_i\leq x_i\leq w_i\;\colon\;i=1,\dots,10.
\end{array}
$$
توجه کنید که یک شرط (قید) -ِ برابری (تساوی) به ازای هر گرهٔ داخلی (گرههایی که $o$ یا $n$ نیستند) داریم. یک گره به دلخواه بردارید. اگر جهتِ همهٔ یالهای متصل به آن به سمت آن میبود، آنگاه شار مثبت یعنی شارهای واردشونده به آن و شارهای منفی یعنی شارهای خارجشونده از آن. پس برای اینکه جمع ورودیها با جمع خروجیها برابر شود کافیست جمع همهٔ شارهای یالهای متصل به آن برابر با صفر باشد. اما اگر یالهایی جهتِ مثبتشان در خلافِ جهت اتصالشان با این گره باشد، آنگاه مثبت یعنی خارجشدن و منفی یعنی واردشدن. پس در جمعِ شارهایِ یالهای متصل به این گره، باید شارِ این یالها را در یک منفی ضرب کنیم و سپس انتظار داشتهباشیم که این جمع برابر با صفر باشد. این دلیل نحوهٔ نوشتهشدنِ شرطهای برابر در بهینهسازیِ بالا است. اگر یالی در سمتِ چپِ گره قرار دارد با علامت مثبت و اگر در سمتِ راستِ آن گره قرار دارد با علامت منفی در جمع ظاهر شدهاست. چون ۵ گرهٔ درونی داریم، پس ۵ شرطِ برابری نیز داریم. برای نمونه شرطِ نخست مربوط به گرهٔ $a$ است. یال یکم در سمت چپ و یالهای چهارم و پنجم در سمت راست آن قرار دارند پس نوشتهایم $x_1-x_4-x_5=0$. و روشن است که یالهای نامتصل به این گره شرکتی در میزان ورودی و خروجی به این گره ندارند پس در شرط نیستند.
دلیلِ تابع هدف و کرانهای گذاشتهشده بر روی مقدار متغیرها هم باید برایتان روشن باشد.
این بهینهسازی را میتوانید با روشهایی که در درس بهینهسازی یادگرفتهاید حل کنید. چون هدفِ اصلیِ این پرسش روش حل کردن بهینهسازی نیست ما در اینجا از زبان برنامهنویسیِ پایتون و دستورِ linprog از بستهٔ scipy همانگونه که در ویدئویی در پستی در بخش بلاگ آموزش دادهشدهاست استفاده میکنیم.
https://math.irancircle.com/blog/418
کُدِ برنامهای که این بهینهسازی را حل میکند به شکل زیر خواهد بود.
# 2022.11.06
# AmirHosein Sadeghimanesh
# Solving a linear integer optimization problem related to the example in
# section 2.2 of the book "Understanding and Using Linear Programming" written
# by Jiri Matousek and Bernd Gartner, Springer, 2007.
from scipy.optimize import linprog
z = [ 0, 0, 0, 0, 0, 0, 0, 0, -1, -1 ]
A = [ [ 1, 0, 0, -1, -1, 0, 0, 0, 0, 0 ],
[ 0, 1, 0, 0, 1, 0, 0, -1, 0, 0],
[ 0, 0, 1, 0, 0, -1, -1, 0, 0, 0],
[ 0, 0, 0, 1, 0, 1, 0, 0, -1, 0],
[ 0, 0, 0, 0, 0, 0, 1, 1, 0, -1] ]
b = [ 0, 0, 0, 0, 0 ]
w = [ 3, 1, 1, 1, 1, 4, 4, 3, 4, 1 ]
problem = linprog( c = z, A_eq = A, b_eq = b,
integrality = [ 1 for i in range( 10 ) ],
bounds = [ ( -w[i], w[i] ) for i in range( 10 ) ],
method = 'highs' )
if problem.success and problem.status == 0:
message = "The problem is solved successfully\nThe maximum flow rate is " +\
str( int( -problem.fun ) ) + ".\nThis maximum can be achieved by x = " +\
str( [ int( problem.x[i] ) for i in range( 10 ) ] ) + "."
else:
message = "The problem is not solved successfully."
print( message )
خروجیِ این برنامه پس از اجرا به شکل زیر خواهد بود.
The problem is solved successfully
The maximum flow rate is 4.
This maximum can be achieved by x = [2, 1, 1, 1, 1, 2, -1, 2, 3, 1].
که برابر با پاسخِ کتاب است. یعنی بیشنهٔ نرخِ شار از گرهٔ $o$ به گرهٔ $n$ برابر با ۴ واحد است که میزان شارها در یالها نیز دادهشدهاست. همهٔ شارها به سمت راست هستند به جز شار در یالِ هفتم که به سمتِ چپ است.