Question

عکس قضیۀ فیثاغورس را با روش برهان خلف اثبات کنید.

عکس قضیۀ فیثاغورس: اگر در یک مثلث با اضلاع $a$، $b$ و $c$، داشته باشیم $a^2 + b^2 = c^2$، آنگاه آن مثلث قائم‌الزاویه است.

یعنی ابتدا فرض کنید مثلث قائم‌الزاویه نیست و زاویۀ 90 درجه ندارد. سپس به نتیجه‌ای خلاف ($a^2 + b^2 = c^2$) برسید که نادرستی فرض اولیه را ثابت می‌کند.

Answer 1

بر طبق قضیۀ کسینوس‌ها خواهیم داشت: $$c^2=b^2+a^2-2ab\cos( \hat{C)}$$ حال طبق رابطه‌ای که داریم، خواهیم داشت: $$c^2=b^2+a^2 \Rightarrow b^2+a^2=b^2+a^2-2ab\cos( \hat{C)}$$ $$\cos( \hat{C} )=0 \Rightarrow \hat{C} =90^ \circ $$

Comments

من قضیه کوسینوس هارو متوجه نشدم. اگر ممکنه یه توضیح درباره تساوی اول بدید. ممنون میشم

Answer 2

@Maria_85 , @Math.Al :

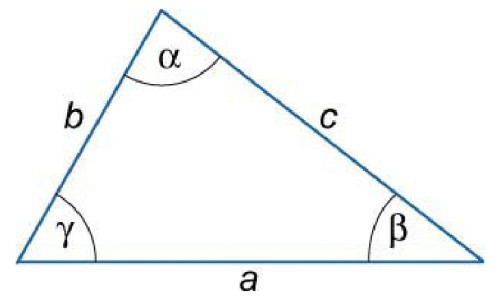
با درود به همراهان گرامی. استاد عزیز @saderi7 به نکته درستی اشاره کردند. به مثلث مختلف‌الزاویه فوق دقت کنید. روابط زیر در آن برقرار است.

$a^2=b^2+c^2-2bc×cos( \alpha )$

$b^2=a^2+c^2-2ac×cos( \beta )$

$c^2=a^2+b^2-2ab×cos( \gamma )$

برای اینکه قضیه فیثاغورث شکل بگیرد، لازم است یکی از بخشهای منفی کسینوسها در روابط فوق صفر شود. این فقط هنگامی ممکن است که یکی از زاوایای $( \alpha , \beta , \gamma )$ نود درجه(قائمه) باشد.بنابراین اگر زاویه نود درجه (قائمه) در مثلثی موجود نباشد، قضیه فیثاغورث شکل نمیگیرد.