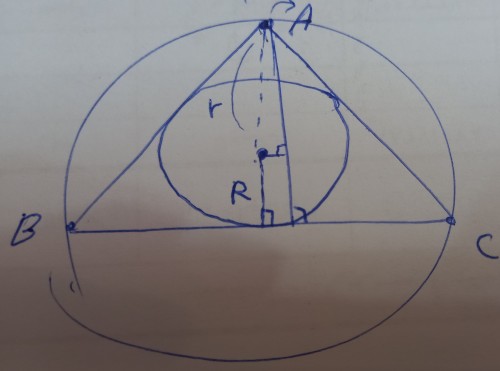
درود ... همانطور که میدونیم r>R پس در نتیجه اگر از مرکز دایره محاطی که o میباشد بر ارتفاع مثل عمود کنیم و راس بالایی مثلث که A هست رو به o وصل کنیم یک مثلث قائم و الزاویه تشکیل میشود که Ao وتر مثلث یا میتوان گفت بزرگترین ضلع مثلث است . حال اگر از o که مرکز دایره محیطی است به قاعده مثلث عمود کنیم میبینیم که پاره خطی هم اندازه با oH پدید می آید. و اگر دقت کنید میبینید که چون بر قاعده مماس است پس oH همان R یا شعاع دایره محیطی است . حال چون oA که شعاع دایره محیطی بود وتر مثلث قائم ما بود و از طول ضلع قائم که جزوی از ارتفاع است بزرگتر است را با R که با oH برابر بود جمع کنیم داریم:r+R >AH+