روشهای گوناگونی را میتوانید پیش بگیرید. نخستین روشی که به ذهن من میرسد به عنوان یک پرسش از درس ریاضی عمومی با فرض اینکه مختصات قطبی را آشنا شدهباشید بازنویسیِ برابریتان به شکل زیر است. که تنها از یک طرفین-وسطین و $x=r\cos\theta$ و $y=r\sin\theta$ استفاده کردهایم.
$$(r^2+\frac{1}{2})^3=16r^5\cos^2\theta\sin^3\theta$$
اکنون با به توان رساندن و مرتب کردن برابریتان همارز با دستگاه زیر میشود.
$$r^6-(16\cos^2\theta\sin^3\theta)r^5-\frac{1}{2}r^4+\frac{1}{4}r^2-\frac{1}{8}=0,\;r>0,\;0\leq\theta < 2\pi$$
اکنون کار سادهاست، یک عدد $n$ به اندازهٔ کافی بزرگ بردارید، بازهٔ $[0,2\pi)$ را به $n$ قسمت مساوی تقسیم و از هر قسمت یک نقطه بردارید، در برابریِ بالا جایگذاری کنید. یک چندجملهای درجهٔ ۶ تکمتغیره بر حسب $r$ دارید. آن را با هر روش دلخواهی حل کنید و پاسخهای حقیقی مثبت آن را بردارید. اگر چند تا پاسخ دارد، همهشان را بردارید و زوجهای مرتب $(\theta,r)$ای که از این طریق بدست میآورید را در یک مجموعه قرار دهید. اکنون مجموعهنقاطتان را در صفحه بگذارید. با افزایش تعداد نقاط شکل حاصل به شکل کامل میل میکند. در پائین دستور یک تابع (الگوریتم) در نرمافزار Mathematica برای انجام این محاسبات و رسم نمودار برای $n$ نقطه که کاربر بدهد را نوشتهام.
PlotOurDiagram[n_] := (
PointsListo = {};
For[i = 1, i <= n, i++,
theta = (i - 1)*2*Pi/n;
rans =
ReplaceAll[
NSolve[r^6 - (16*Cos[theta]^2*Sin[theta]^3)*r^5 - r^4/2 +
r^2/4 - 1/8 == 0 && r > 0, r, Reals][[1]]][r];
AppendTo[PointsListo, {rans*Cos[theta], rans*Sin[theta]}];
];
Return[ListLinePlot[PointsListo, PlotRange -> {{-3, 3}, {-1, 3}},
PlotStyle -> Red]];
)
برای اینکه غیر از رسمشدن، زمان انجام این محاسبه و رسم را هم متوجه شویم از دستور Timing مانند زیر استفاده کردهام. $n$ را نیز ۱۰۰ دادهام. زمانی که از Timing استفاده میکنید، یک لیست دو عضوی میگیرید که عوض نخست یک عدد که مدت زمان را نشان میدهد است و عضو دوم خروجی تابعی که به Timing دادهبودید.
ploto100 = Timing[PlotOurDiagram[100]]
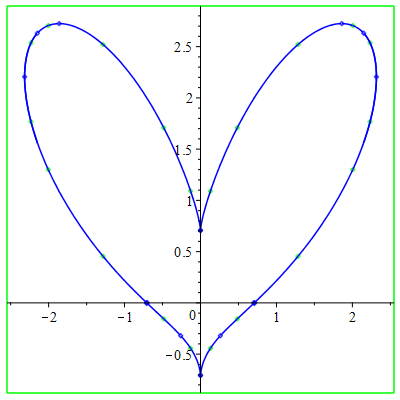
زمان انجام این محاسبه بر روی رایانهام تقریبا $0.17$ ثانیه است. شکل حاصل در زیر آوردهشدهاست.
خیلی شکل خوبی نیست ولی باید توجه داشت که در این فرآیند چندین نکتهٔ آنالیز عددی (از حل عددی برابری چندجملهای تا خود ترسیم و تقسیمبندی و دقت اعشاری محاسبات) وجود دارد که برای دقیقتر شدن شکل باید آنها را بررسی کرد. به هر حال با یک چشمپوشی بزرگ میتوان آن را تقریبی از شکلی که آقای @fardina رسمکردهاند در نظر گرفت.
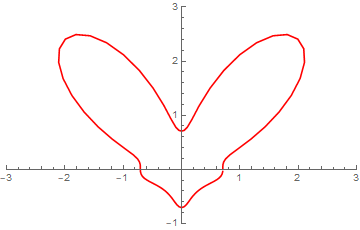
میتوانید برای چککردن از دستورِ حاضر و آمادهٔ نرمافزار Mathematica برای رسم مجموعهتراز که برای رسم مجموعهٔ $(x,y)$هایی که در یک برابری $f(x,y)=0$ صدق کنند تهیه شده استفاده کنید، این دستور ContourPlot است.
ContourPlot[(x^2 + y^2 - 1/2)^3 - 16*x^2*y^3 == 0, {x, -3, 3}, {y, -1,
3}, PlotRange -> {{-3, 3}, {-1, 3}}, ContourStyle -> RGBColor[1, 0, 0]]
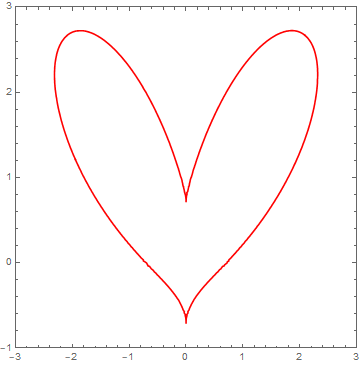
موتوری که آقای @fardina برای ترسیم استفاده کردهاند نیز موتور یکسانی است.
دستور plot_real_curve از بستهٔ algcurves در نرمافزار Maple نیز شکل قلبگونه را میدهد. این دستور برای رسم خمها در صفحه به کار میرود.
algcurves[plot_real_curve]((x^2+y^2-1/2)^3-16*x^2*y^3,x,y);